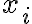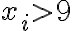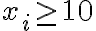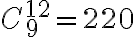Hola buenas! Quisiera saber si mi razonamiento está bien para el ejercicio 6):
Primero hice el caso general, en el cual no hay restricciones: N(U)=CR(7,31);
Luego hice las restricciones opuestas:
Ci : casos de los que cumplen que x1+x2+x3+x4+x5+x6+x7 = 31 con xi>=9; N(Ci)=CR(7,22);
CiCj (con i != j) : casos de los que cumplen que x1+x2+x3+x4+x5+x6+x7=31. con xi,xj>=9; N(CiCj)=CR(7,13);
CiCjCk (con i != j != k): casos de los que cumplen que x1+x2+x3+x4+x5+x6+x7=32,
con xi,xj,xk mayores o iguales a 9, N(CiCjCk)=CR(7,4);
Por lo tanto, la cantidad de enteros que cumplen que la suma de de sus dígitos sea igual a 31 son:
N(U)-C(7,1)(N(Ci)+C(7,2)(N(CiCj))-C(7,3)(N(CiCjCk)) =CR(7,31)-C(7,1)CR(7,22)+C(7,2)CR(7,13)-C(7,3)CR(7,4).
También quería sacarme una duda del resultado del ejercicio 5, ya que me dió 455 formas en total pero no estoy seguro si está bien el resultado, la forma de razonarlo fue similar al ejercicio 6.