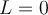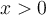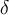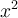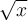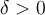Buenas tardes
Estoy intentando realizar esta parte y otros ejercicios de 4.2.2, no comprendo como debería aplicar la definición de límites para resolverlos. Entiendo que al darme un epsilon, yo debo hallar L y delta (el cual depende de epsilon dado), la parte de hallar L la he podido hacer. Lo que se me dificulta es hallar delta, no comprendo como hallar delta a partir de las inecuaciones, mismo problema me ocurre con otros ejercicios de esta parte. Tal vez si tuvieras algún ejemplo podría entenderlo. Muchas gracias.
Saludos, Pablo