Buenos dias,
Quería consultar como puedo resolver el ejercicio. Según mi razonamiento, supuse que tomar en cuenta la definición de límite y despejar delta seria lo correcto. Sin embargo, no se como comenzarlo.
Buenos dias,
Quería consultar como puedo resolver el ejercicio. Según mi razonamiento, supuse que tomar en cuenta la definición de límite y despejar delta seria lo correcto. Sin embargo, no se como comenzarlo.
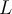 y un
y un 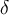 que cumpla que si
que cumpla que si 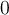 entonces
entonces  . Mi recomendación es que primero pienses en el
. Mi recomendación es que primero pienses en el 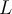 que te va a servir , pensando a qué se acerca la función que te dan cuando te "acercas " 0 . Despúes que tengas el
que te va a servir , pensando a qué se acerca la función que te dan cuando te "acercas " 0 . Despúes que tengas el 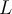 , es importante recalcar que se pide un
, es importante recalcar que se pide un 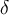 que te sirva, no el mayor ni nada por el estilo. Siendo esto así, ahora sí pensalo de "atrás para adelante", vos tenes que
que te sirva, no el mayor ni nada por el estilo. Siendo esto así, ahora sí pensalo de "atrás para adelante", vos tenes que  y queres acotar el valor absoluto de x, entonces por ejemplo podes hacer lo siguiente :
y queres acotar el valor absoluto de x, entonces por ejemplo podes hacer lo siguiente :  ahora, si le pedís a esto último que sea menor que 10^-5, en particular el valor absoluto de la izquierda es menor a 10^-5. Entonces ahora el problema se redujo a hallar un
ahora, si le pedís a esto último que sea menor que 10^-5, en particular el valor absoluto de la izquierda es menor a 10^-5. Entonces ahora el problema se redujo a hallar un 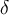 que cumpla que
que cumpla que  y bueno, por ejemplo
y bueno, por ejemplo  va a funcionar ( te dejo que lo compruebes por tu cuenta).
va a funcionar ( te dejo que lo compruebes por tu cuenta). Buenas
Buenas, la definición que damos en las notas permite definir limites en el "borde" del dominio como es el caso (Definición 9 de las notas).
Sin embargo no es lo que pide explicitamente el ejercicio.
El ejercicio debería decir o bien  como tu mencionas y como esta en el ejercicio anterior, o bien tomar solo los
como tu mencionas y como esta en el ejercicio anterior, o bien tomar solo los 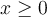 .
.
Utiliza cualquier de los modos para realizar el ejercicio. El ejercicio se corregirá en breve
Saludos
Buenas tardes
Estoy intentando realizar esta parte y otros ejercicios de 4.2.2, no comprendo como debería aplicar la definición de límites para resolverlos. Entiendo que al darme un epsilon, yo debo hallar L y delta (el cual depende de epsilon dado), la parte de hallar L la he podido hacer. Lo que se me dificulta es hallar delta, no comprendo como hallar delta a partir de las inecuaciones, mismo problema me ocurre con otros ejercicios de esta parte. Tal vez si tuvieras algún ejemplo podría entenderlo. Muchas gracias.
Saludos, Pablo
 , y en la parte a el límite es
, y en la parte a el límite es 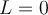 . Esta función está definida sólo para
. Esta función está definida sólo para 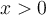 . Entonces queremos hallar
. Entonces queremos hallar 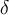 de modo que, si
de modo que, si  se cumpla que
se cumpla que  . Como tanto
. Como tanto 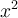 como
como 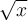 son funciones crecientes,
son funciones crecientes,  . Entonces, nos va a servir cualquier
. Entonces, nos va a servir cualquier 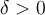 para el cual
para el cual  .
.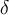 más grande posible. El más grande posible sería el que cumple
más grande posible. El más grande posible sería el que cumple  *.
*. . Para que pase esto,
. Para que pase esto, 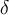 debe ser menor que 1, por lo que
debe ser menor que 1, por lo que  . Así que nos alcanza con encontrar un
. Así que nos alcanza con encontrar un 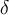 para el cual
para el cual  . Por ejemplo,
. Por ejemplo,  funciona.
funciona. 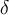 que satisface esta ecuación. Sugerencia: pensá en el Teorema de Bolzano.)
que satisface esta ecuación. Sugerencia: pensá en el Teorema de Bolzano.)