Práctico 4 - Foro de consultas

Buenas.

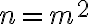Por definición, $n$ es cuadrado perfecto si se puede escribir como el cuadrado de algún número natural: $n=m^2$, para algún 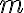$m$ natural.

Por ejemplo, 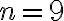$n=9$ es cuadrado perfecto, pues 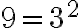$9=3^2$ (en este caso $m=3$).

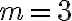El ejercicio pide hallar el menor natural n que cumple las siguientes dos condiciones a la vez:

1. $n$ es cuadrado perfecto, y
2. 7! divide a $n$.

Esta es la consigna. Si aún no se entiende la consigna, pregunta de nuevo.

Con respecto a cómo resolver el ejercicio: la idea es usar que un número es cuadrado perfecto, si y sólo sí todas las potencias de sus factores primos son múltiplos de 2. A esto hay que combinarlo con la definición de divisible.

Te doy una pista: si 7! fuese cuadrado perfecto, entonces el número buscado sería n=7!. Como 7! no es cuadrado perfecto, hay que arreglarlo un poco.

Saludos.