Hola, tengo dificultades para entender cómo funciona f1 , qué significa la regla de asociación. Además, si no es molestia me gustaría preguntar qué significan los paréntesis rectos en las otras dos funciones del mismo ejercicio, no entiendo, en el caso de ser intervalos, cómo están incluidos en las funciones. Desde ya muchas gracias.
Buenas
Primero te comento lo de la función ![f(x) = [x] f(x) = [x]](https://eva.fing.edu.uy/filter/tex/pix.php/d770db0bd6e7af05f6bbbbc8edf51ade.png) . en estas secciones del practico la función
. en estas secciones del practico la función ![f(x) = [x] f(x) = [x]](https://eva.fing.edu.uy/filter/tex/pix.php/d770db0bd6e7af05f6bbbbc8edf51ade.png) es la distancia al/los enteros mas cercanos. Esa definición esta en el ejercicio 3.1-1. Evaluando en algunos puntos para entender mejor
es la distancia al/los enteros mas cercanos. Esa definición esta en el ejercicio 3.1-1. Evaluando en algunos puntos para entender mejor  .
.
Claro que para el ejercicio tendras que entender como es el gráfico. Si tienes dudas sobre esta funcion vuelve a escribir
De nuevo para entender un poco de la funcion evaluemos en algunos puntos.
Por ejemplo  y
y  . Es decir la funcion
. Es decir la funcion 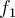 en un valor
en un valor  toma el mas grande de los elementos entre
toma el mas grande de los elementos entre  y
y  (podrian ser iguales), como vimos en los ejemplos esto depende de
(podrian ser iguales), como vimos en los ejemplos esto depende de  claramente, pero para un
claramente, pero para un  concreto esta da un número concreto.
concreto esta da un número concreto.
Tenemos entonces que la funcion 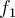 se puede pensar como un función "partida".
se puede pensar como un función "partida".
Por lo que debes entender cuando  . Esa inecuacion es equivalente a
. Esa inecuacion es equivalente a 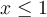 , es decir
, es decir
Más alla de que despues debas encontrar los puntos de corte, una forma de entender la situación es observar el grafico de las funciones en cuestión
si notamos  y
y  la función es
la función es  . si bosquejamos las funciones
. si bosquejamos las funciones  y
y 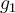

Puedes ver que la funcion  es mayor que
es mayor que 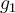 a partir de
a partir de  , luego
, luego  para todo
para todo  . Y para
. Y para 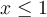 , es
, es 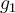 la que es mayor o igual a
la que es mayor o igual a  . La funcion
. La funcion 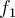 quedarse con el grafico "que este mas arriba de las dos".
quedarse con el grafico "que este mas arriba de las dos".
Si tienes dudas vuelve a consultar
Saludos
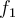



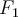
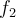

![n \leq x \leq n+0.5 \Rightarrow [x] = x-n n \leq x \leq n+0.5 \Rightarrow [x] = x-n](https://eva.fing.edu.uy/filter/tex/pix.php/c4a4f4136d14cbf96374520710f61a65.png)
![n+0.5 < x < n+1 \Rightarrow [x] =n+1- x n+0.5 < x < n+1 \Rightarrow [x] =n+1- x](https://eva.fing.edu.uy/filter/tex/pix.php/fe30f111ec85e60f808fafcfb98f1afc.png)


