Ejercicio 9 - Parte 4

Ejercicio 9 - Parte 4

de Karina Valeria Marrero Moraiz -
Número de respuestas: 3

Buenas tardes, haciendo el Práctico 1 encontré que el resultado que yo obtuve del Ejercicio 9.4 () no coincide con el resultado que hay en el pdf "Respuestas al Práctico 1: Operaciones": y no logro encontrar el error.

Mi resultado fue el siguiente: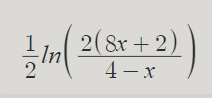 

¿Podrían ayudarme a reconocer en qué pude haber fallado, o quizá mostrarme el desarrollo de este problema para compararlo con el mío?

Muchas gracias!

En respuesta a Karina Valeria Marrero Moraiz

Re: Ejercicio 9 - Parte 4

de Juan Manuel Cabrera -

Hola, Karina.

Si envias una imagen de tu resolución es más fácil detectar en dónde está el error.

A simple vista puedo decirte que ese 2 multiplicando dentro del argumento del Ln debería ser un 4, tal como en la solución. 

Eso es porque en la solución expresan el 2 como raíz cuadrada de 4, para poder tener todo el argumento dentro de la raíz cuadrada y recién ahí "sacar" el 1/2 multiplicando fuera del Ln. 

En otras palabras: Si tengo Ln(a.b^1/2), eso no es igual a 1/2.Ln(a.b). Primero, debo operar dentro del argumento para tener todo elevado a la 1/2. Es decir:  \ln(a \cdot b^{1/2}) = \ln(\sqrt{a^2 \cdot b}) = \frac{1}{2} \ln(a^2 \cdot b) 

Espero haberme explicado bien.

Saludos!
En respuesta a Juan Manuel Cabrera

Re: Ejercicio 9 - Parte 4

de Karina Valeria Marrero Moraiz -
Hola Juan Manuel!

Gracias por la explicación, volví a hacer el ejercicio pasando el 2 de ln(2) a raíz cuadrada de 4 y pude conseguir el mismo resultado que el archivo de las soluciones.

Te dejo por acá abajo el desarollo que hice yo y las propiedades que utilicé. ¿Es necesario pasar el ln(2) a raíz cuadrada o es posible que el resultado que me dio al principio también se pueda considerar una respuesta correcta? Me gustaría saberlo para no volver a cometer el mismo error en el futuro.

Resolución ejercicio 9.4 Práctico 1

Muchas gracias por la ayuda!

Saludos.
En respuesta a Karina Valeria Marrero Moraiz

Re: Ejercicio 9 - Parte 4

de Juan Manuel Cabrera -

Buenas!

El problema en la resolución está en el último paso. 

Lo que sabemos es que \log(a) + \log(b) = \log(a \cdot b)

Sin embargo, en general, \frac{1}{2}\log(a) + \log(b) \neq \log(a \cdot b) \neq \frac{1}{2}\log(a \cdot b)

Es por eso que tengo que buscar que ambos términos me queden multiplicados por 1/2 para sacarlo de denominador común, y recién ahí aplicar la propiedad de la suma de logaritmos. Por eso se hace ese "juego" con el Ln(2) en la solución.

Saludos!