Buenas tardes
El cálculo de la cantidad de particiones con esas características en función de n me quedó como el producto de los primeros n impares. Consulto para ver si es correcto, porque fue bastante rebuscado y le pude errar feo.
Buenas tardes
El cálculo de la cantidad de particiones con esas características en función de n me quedó como el producto de los primeros n impares. Consulto para ver si es correcto, porque fue bastante rebuscado y le pude errar feo.
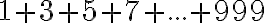 vas a poner como respuesta
vas a poner como respuesta 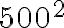 en vez de toda esa suma.
en vez de toda esa suma.Buen día
Gracias Claudio por la pronta y tan detallada respuesta.
Se entiende la letra, así que le erré en algún razonamiento.
Mando captura y explico.

Intenté hallar la cantidad de particiones (an) por recurrencia. O sea responder a la pregunta qué sucede cuando agrego dos elementos más, en cuanto a la cantidad de particiones . En primera instancia agregar a cada una de las particiones anteriores un conjunto de los nuevos 2 elementos genera parte de lo que quiero calcular( an+1 = an + ** ). A esto agregar la posibilidad de intercambiar de “lugar” a cada uno de los nuevos elementos por los 2n anteriores. Cuantas veces puedo hacer eso: 2n veces . quedando an+1= an + an . 2n
Ene el ejemplo se ilustra mejor el razonamiento
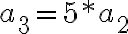 y da una buena idea de que se generaliza para cualquier n como
y da una buena idea de que se generaliza para cualquier n como 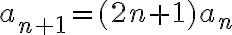 para todo
para todo 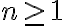 donde
donde  es la cantidad de formas de particionar
es la cantidad de formas de particionar 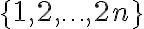 en subconjuntos de tamaño 2. Entonces lo que tendrías que mostrar es que si consideramos una partición de
en subconjuntos de tamaño 2. Entonces lo que tendrías que mostrar es que si consideramos una partición de 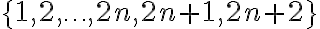 en subconjuntos de tamaño 2 (que por definición hay
en subconjuntos de tamaño 2 (que por definición hay 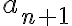 de tales particiones) entonces hay exactamente
de tales particiones) entonces hay exactamente  particiones que contienen el par
particiones que contienen el par 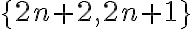 y para cada
y para cada 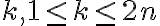 fijo, también existen exactamente
fijo, también existen exactamente  particiones que contienen al par
particiones que contienen al par 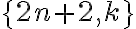 . De esa forma concluyes que
. De esa forma concluyes que 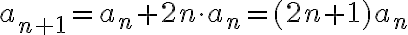 . Como
. Como 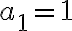 entonces te queda
entonces te queda 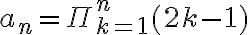 que es la solución del problema.
que es la solución del problema.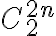 formas de seleccionar dos elementos para el primer par, luego
formas de seleccionar dos elementos para el primer par, luego 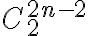 para el segundo par, etc... por la regla del producto tenemos el producto de esas posibilidades. La solución será ese producto dividido n! por lo que dijimos antes dado un total de
para el segundo par, etc... por la regla del producto tenemos el producto de esas posibilidades. La solución será ese producto dividido n! por lo que dijimos antes dado un total de 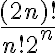
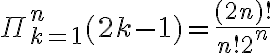 .
.