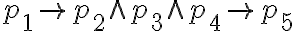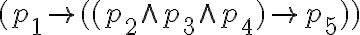Quería chequear los resultados:
a. No se abrevia a ninguna fórmula de PROP ya que es una conjunción de cinco variables proposicionales distintas: p1, p2, p3, p4, y p5.
b. No se abrevia a ninguna fórmula de PROP ya que contiene una implicación seguida de una conjunción, lo cual no es una estructura simple que se encuentre en las fórmulas de lógica proposicional.
c. Esta fórmula se abrevia a la forma más básica de implicación: p → q, donde p es la disyunción (p1 ∨ p2) y q es p3.
d. No se abrevia a ninguna fórmula de PROP ya que contiene una implicación seguida de una conjunción, similar al caso de la fórmula b.
e. No se abrevia a ninguna fórmula de PROP ya que es una conjunción de una implicación (p1 → p2) y una conjunción (p3 ∧ p4), lo cual no es una estructura simple en la lógica proposicional.
f. Esta fórmula se abrevia a la forma básica de implicación: p → q, donde p es la negación de la disyunción (¬(p1 ∨ p2)) y q es p3.
Saludos.