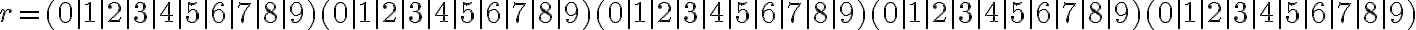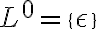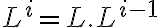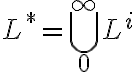Hola Iván,
no, no se puede hacer eso. Si querés 5 números cualquiera seguidos, entonces la expresión regular es (perdón por la redundancia, pero es para dejarlo claro):
es (perdón por la redundancia, pero es para dejarlo claro):
no, no se puede hacer eso. Si querés 5 números cualquiera seguidos, entonces la expresión regular
 es (perdón por la redundancia, pero es para dejarlo claro):
es (perdón por la redundancia, pero es para dejarlo claro):Hacer 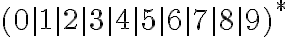 no sería válido, pues eso te daría una secuencia de 0 o más números. Particularmente sí que podés generar una secuencia de 5 números, pero también vas a tener secuencias de 4, de 6, de 8, de 135 y de ningún número (al generarse la tira vacía
no sería válido, pues eso te daría una secuencia de 0 o más números. Particularmente sí que podés generar una secuencia de 5 números, pero también vas a tener secuencias de 4, de 6, de 8, de 135 y de ningún número (al generarse la tira vacía 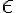 ).
).
Acordate que la definición de clausura de Kleene de un lenguaje L es:
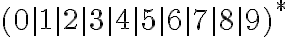 no sería válido, pues eso te daría una secuencia de 0 o más números. Particularmente sí que podés generar una secuencia de 5 números, pero también vas a tener secuencias de 4, de 6, de 8, de 135 y de ningún número (al generarse la tira vacía
no sería válido, pues eso te daría una secuencia de 0 o más números. Particularmente sí que podés generar una secuencia de 5 números, pero también vas a tener secuencias de 4, de 6, de 8, de 135 y de ningún número (al generarse la tira vacía 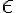 ).
).Acordate que la definición de clausura de Kleene de un lenguaje L es:
Cualquier consulta a las órdenes,
Santi
Santi