Buenas!
Estuve
haciendo el ejercicio 9), y se me ocurrió una posible forma de
demostrar el paso inductivo de la inclusión, que de ser correcta me
parece mas intuitiva/mas directa que aplicar dos veces el PIP. Pero no sé si voy por buen camino o tiene sentido.
Queremos
probar que 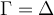 y para eso se prueba la doble
inclusión. Supongamos que primero quiero probar que
y para eso se prueba la doble
inclusión. Supongamos que primero quiero probar que 
Para aplicar el PIP, defino una propiedad  . Y se quiere probar
. Y se quiere probar  . Utilizo el PIP en
. Utilizo el PIP en 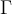 .
.
El paso base es trivial, pues 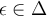 por def.
por def.
La
idea viene para el paso inductivo, donde suponemos que  , y queremos probar entonces
, y queremos probar entonces  .
.
Ya que  conjunto de reglas que, aplicándolas en cierto orden, y
usando la def. de
conjunto de reglas que, aplicándolas en cierto orden, y
usando la def. de 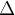 construyen a
construyen a 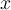 . La idea es tomar
ese conjunto de reglas, y añadir al principio de ellas las reglas para
crear
. La idea es tomar
ese conjunto de reglas, y añadir al principio de ellas las reglas para
crear  . Y que al aplicar dichas reglas y luego
. Y que al aplicar dichas reglas y luego 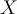 en el orden
correcto, la tira construida es
en el orden
correcto, la tira construida es  , entonces quedaría demostrado
, entonces quedaría demostrado  , pues
, pues  es construible usando las reglas de
es construible usando las reglas de 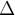 , si
se da la HI.
, si
se da la HI.
También quiero notar que la intuición que
tuve es que, para añadir a cualquier elemento  , se
necesita "pasar" por la primera regla (la de la tira vacía) o tener algo
ya en
, se
necesita "pasar" por la primera regla (la de la tira vacía) o tener algo
ya en  , porque sino el antecedente de las otras reglas
nunca se cumple, y por tanto no se pueden aplicar, pero simplemente se
podría cambiar esa primera regla por las reglas que sirven para añadir a
, porque sino el antecedente de las otras reglas
nunca se cumple, y por tanto no se pueden aplicar, pero simplemente se
podría cambiar esa primera regla por las reglas que sirven para añadir a
 en
en 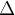
Sé que le falta formalidad, solo quería explicar la idea antes de intentar formalizar todo para ver si voy por buen camino.