No se me estaría ocurriendo por donde empezar empezar a encarar el ejercicio. ¿Hay que verificar con valores aleatorios o hay que hacer algún tipo de demostración?
Copio la primera parte de la letra: sean 
, 
, 
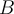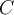y 
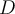conjuntos. Verificar que 
.
Yo diría que tenés que escribir una prueba. Abajo te doy indicaciones de cómo armarla. Dejo espacios en blanco para que completes lo que falta. Antes de empezar, corroborá que sepas bien cuáles son las definiciones de unión y producto cartesiano entre conjuntos.
Prueba: para probar la inclusión, hay que probar que todos los elementos de
también están en 
. Así que tomo un 
cualquiera, y hay probar que se cumple 
.
Por definición de unión, hay dos casos: que
, o que 
. Así que uno puede hacer la prueba en cada caso.
Caso 1: supongamos que. Entonces, por definición de producto cartesiano, 
cumple que .............. e 
cumple que .............. . Por lo tanto, 
e 
. Esto concluye la prueba del Caso 1 porque ..............
Caso 2: supongamos que. Entonces ........................................................................................................................................................................ . Esto concluye la prueba del Caso 2.
Fin de la prueba.
En la otra parte del ejercicio, tenés que buscar un ejemplo concreto en donde se dé la inclusión estricta, y uno en el que se dé la igualdad entre los conjuntos.
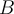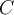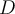, , y conjuntos. Verificar que .Yo diría que tenés que escribir una prueba. Abajo te doy indicaciones de cómo armarla. Dejo espacios en blanco para que completes lo que falta. Antes de empezar, corroborá que sepas bien cuáles son las definiciones de unión y producto cartesiano entre conjuntos.
Prueba: para probar la inclusión, hay que probar que todos los elementos de
también están en . Así que tomo un cualquiera, y hay probar que se cumple .Por definición de unión, hay dos casos: que
, o que . Así que uno puede hacer la prueba en cada caso.Caso 1: supongamos que
. Entonces, por definición de producto cartesiano, cumple que .............. e cumple que .............. . Por lo tanto, e . Esto concluye la prueba del Caso 1 porque ..............Caso 2: supongamos que
. Entonces ........................................................................................................................................................................ . Esto concluye la prueba del Caso 2.Fin de la prueba.
En la otra parte del ejercicio, tenés que buscar un ejemplo concreto en donde se dé la inclusión estricta, y uno en el que se dé la igualdad entre los conjuntos.