Buenas, en general es posible probar que  es
es  ? Mi duda viene a partir de este ejercicio de cuestionario. Sé que es el mismo ejercicio del examen pasado con
? Mi duda viene a partir de este ejercicio de cuestionario. Sé que es el mismo ejercicio del examen pasado con  pero no creo que se me ocurra la forma que hay para resolverlo en la solución
pero no creo que se me ocurra la forma que hay para resolverlo en la solución

Buenas.
En caso de que haya sido un error de tipeo, se puede demostrar que  (es decir, la suma, no la resta) es de orden
(es decir, la suma, no la resta) es de orden  . Es parte de la demostración de que el método del trapecio es de segundo orden, y también como señalas es parte de la demostración del examen que realizaba la combinación convexa de los métodos de Euler hacia adelante y hacia atrás, del cuál el método del trapecio es un caso así como el del cuestionario que muestras.
. Es parte de la demostración de que el método del trapecio es de segundo orden, y también como señalas es parte de la demostración del examen que realizaba la combinación convexa de los métodos de Euler hacia adelante y hacia atrás, del cuál el método del trapecio es un caso así como el del cuestionario que muestras.
La demostración en resumen es:
Si realmente te referías a la resta... podrías llegar a reducir a algo de este tipo:
Habría que ver mejor llegado a ese punto cómo es que el método define  , pero no parece que se pueda probar nada en términos absolutamente generales.
, pero no parece que se pueda probar nada en términos absolutamente generales.
Igualmente no estoy viendo, si fuera ese el caso, la aplicación de esa propiedad a la pregunta del cuestionario que señalabas.
Saludos.
 , por lo que debería ser al menos de orden
, por lo que debería ser al menos de orden 
 , donde
, donde 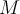 esté acotada, en particular si es alguna combinación lineal de
esté acotada, en particular si es alguna combinación lineal de  evaluada en diferentes puntos del intervalo en cuestión.
evaluada en diferentes puntos del intervalo en cuestión. con
con 
 sea por lo menos
sea por lo menos 
Hola Juan Agustín.
No sé si se entendió mi otro mensaje.
Para este método en particular (y algunos otros parecidos) podrías argumentar:
El último término,  , desaparece con
, desaparece con  por continuidad de
por continuidad de  .
.
El término  está acotado por continuidad de
está acotado por continuidad de  (Weierstrass).
(Weierstrass).
Con eso deberías poder terminar la prueba que estabas haciendo.
Saludos.