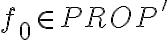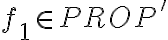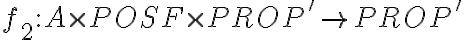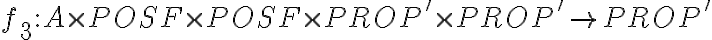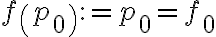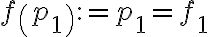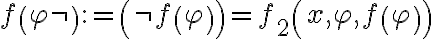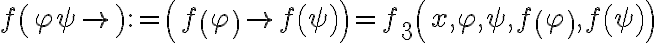Hola. Estaba haciendo este ejercicio pero me surgio una duda en la parte b.
Primero planteé el ERP para POSF como sigue:
Sea A el alfabeto definido en la parte a y PROP' el conjunto inductivo definido en la parte a, y sean:
Entonces existe una única funcion 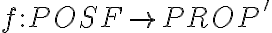 tal que:
tal que:
Ahora, ¿como pruebo que es invertible (antes de definir la que viene)? Veo que hay una correspondencia uno a uno pero formalmente como deberia mostrarlo? Gracias