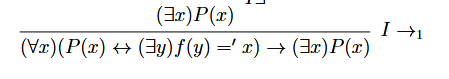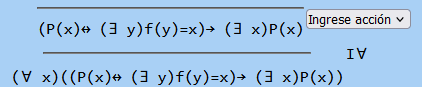Hola Guido:
El yoda se comporta en algunos casos un poco diferente a lo que
vemos en el curso.
En nuestro curso, el cuantificador tiene mayor precedencia (es más fuerte) que
la flecha. Ser más fuerte significa que liga primero. Para entenderlo mejor,
observemos que tradicionalmente la multiplicación tiene mayor precedencia
que la suma (y no al revés).
Así, si tenemos:
4 × 5 + 7
se debe interpretar como: (4 × 5) + 7.
Como la multiplicación tiene mayor precedencia, liga antes que la suma.
Si vamos ahora a la lógica de predicados. Suponemos:
(∀x) ϕ → ψ
se va a interpretar como ( (∀x) ϕ) → ψ
Es decir, el cuantifiador liga primero por ser más fuerte.
Por lo que veo, el yoda tiene la precedencia invertida y parece ser más
fuerte la flecha que el cuantificador.
Ante la duda, se recomienda poner todos los paréntesis y no preocuparnos
por la precedencia.
Para eso, deberías entrar en el yoda la fórmula parentizada:
((All x) ( P(x) <-> (Exi y) f(y) = x)) -> (Exi x) P(x)
agregando paréntesis para hacer que ligue primero el cuantificador
y de esa manera, el conectivo principal será el implica.