Hola, tengo una duda sobre la resolución de este ejercicio. Porque dice que el limite de g en (0,0) existe poque al hacerle el cambio a polares a la funcion f, que seria g, nos acercamos por rectas de la forma y=mx. Pero segun lo que yo entiendo, al hacer el cambio a polares, nos acercamos por cualquier direccion y no unicamente por rectas, por lo tanto el limite no existiria como el de f.
Hola Ayelén,
Generalmente cuando se hacer referencia al límite en polares, lo que se está haciendo referencia es a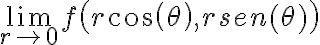
con 
fijo. Esto es equivalente a tomar el límite por rectas, donde es el ángulo de la recta. Se podría usar polares para acercarnos de otras formas, dado que en realidad la función 
es un cambio de coordenadas, y podríamos acercarnos por ej en espirales por decir una forma en la que nos ayudaría utilizar polares. Pero como mencionaba al principio, el texto se refiere a acercarse por rectas, y ahí no alcanza con que esos límites siempre den 
, como marca este ejercicio por ejemplo.
Si no se entiende algo o tenés algún comentario respondé nomás y la seguimos.
Saludos,
Leandro
Generalmente cuando se hacer referencia al límite en polares, lo que se está haciendo referencia es a
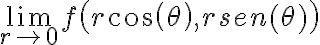con fijo. Esto es equivalente a tomar el límite por rectas, donde es el ángulo de la recta. Se podría usar polares para acercarnos de otras formas, dado que en realidad la función es un cambio de coordenadas, y podríamos acercarnos por ej en espirales por decir una forma en la que nos ayudaría utilizar polares. Pero como mencionaba al principio, el texto se refiere a acercarse por rectas, y ahí no alcanza con que esos límites siempre den , como marca este ejercicio por ejemplo.Si no se entiende algo o tenés algún comentario respondé nomás y la seguimos.
Saludos,
Leandro
Hola, entonces en este caso la función g estaría definida con un 𝜃 fijo? por eso el limite da 0? siempre que se define a la función con el cambio a coordenadas polares es con un ángulo fijo o solo en este caso? porque como define g con las variables,𝜃 y r yo entendía que ambas estaban variando al no especificar en la letra que el ángulo quedaba fijo. Gracias
La función se define para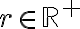 
y ![\theta \in [0,2\pi]](https://eva.fing.edu.uy/filter/tex/pix.php/3245ef4df4d41ae74886458677dddef7.png "\theta \in [0,2\pi]")
, es decir, no es que haya una variable fija. Luego lo que en general hacemos es tomar el límite con 
tendiendo a y fijo, que eso equivale a moverse por la recta de ángulo . Cuando decimos que el límite por polares da 
lo que decimos es que cada uno de los límites con fijo y tendiendo a lo hace, no es algo de la letra sino es a lo que llamamos límite por polares en general. En conclusión, la función se define con ambas variables pero luego generalmente la usamos sólo en límites con fijo.
Lo que no me termina de quedar claro es por que entonces cuando hacemos un limite por polares y nos da 0, decimos que existe en cualquier direccion el limite. Porque si en realidad estamos fijando angulos, existe acercamos por rectas con ese angulo pero no en cualquier direccion. Muchas gracias
Porque "el límite en cualquier dirección" refiere a el límite direccional en cualquier dirección. Cuando nos acercamos por otras curvas, como parábolas, no nos referimos a ellas como direcciones, sino que las direcciones son las rectas por las que nos podemos acercar.
Pero si las direcciones son las rectas entonces no podes afirmar que si el limite por polares nos da 0 quiere decir que la funcion tiene limite en ese punto? Porque yo tenia entendido que si el limite en polares existia entonces queria decir que existia el limite independiententemente de como me acercara al punto pero en este caso el limite en polares me dice que existe pero no existe el limite si te acercas por la direccion entre las dos parabolas. No entiendo por que eneste caso hacer el limite por polares y que exista no me permite afirmar que existe el limite cuando en otros ejercicios lo hacemos. Gracias
Que los límites direccionales existan y coincidan no alcanza para que exista el límita, esto es independiente a si los calculamos por polares o parametrizando las rectas. Lo que utilizamos en polares es la propiedad del ejercicio 4e del práctico 7, que para las hipótesis que menciona sí podemos deducir que el límite es .
.