Buenas, para asegurar la convergencia de un MIG es necesario que la norma de g' sea menor a 1 en un entorno de x*, pero si tengo g' mayor o igual a 1 se asegura la no convergencia del método?
Gracias!
Hola Leandro,
Creo que tu pregunta se solapa un poco con esta otra:
https://eva.fing.edu.uy/mod/forum/discuss.php?d=278966
En concreto, si y
y 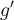 es continua en un entorno de
es continua en un entorno de  , entonces
, entonces  para todo
para todo  en algún entorno de
en algún entorno de  y la iteración no va a converger. Probá pensar un ejemplo en el que
y la iteración no va a converger. Probá pensar un ejemplo en el que  y la iteración sea convergente, y otro en el que no lo sea. Lo lindo de este curso es que después de pensar los ejemplos, los podés implementar y experimentar.
y la iteración sea convergente, y otro en el que no lo sea. Lo lindo de este curso es que después de pensar los ejemplos, los podés implementar y experimentar.
Creo que tu pregunta se solapa un poco con esta otra:
https://eva.fing.edu.uy/mod/forum/discuss.php?d=278966
En concreto, si
 y
y 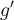 es continua en un entorno de
es continua en un entorno de  , entonces
, entonces  para todo
para todo  en algún entorno de
en algún entorno de  y la iteración no va a converger. Probá pensar un ejemplo en el que
y la iteración no va a converger. Probá pensar un ejemplo en el que  y la iteración sea convergente, y otro en el que no lo sea. Lo lindo de este curso es que después de pensar los ejemplos, los podés implementar y experimentar.
y la iteración sea convergente, y otro en el que no lo sea. Lo lindo de este curso es que después de pensar los ejemplos, los podés implementar y experimentar.Hola, entonces se podría decir que un MIG converge si y solo si |g'(x*)|<1? Porque como dijo Leandro, en las notas solo está la implicancia hacia un lado.
Hola Nicolás,
No, no es un si y sólo si. Podés tener convergencia incluso si , pero si
, pero si  no podés garantizar la convergencia.
no podés garantizar la convergencia.
Un par de ejemplos sencillos es aproximar la raíz para las iteraciones
para las iteraciones  y
y  . En ambos casos tenés
. En ambos casos tenés  , pero en uno la derivada es menor a 1 en un entorno de
, pero en uno la derivada es menor a 1 en un entorno de  y en el otro es mayor. Probá (implementando) qué pasa con esas iteraciones si las inicializás cerca de
y en el otro es mayor. Probá (implementando) qué pasa con esas iteraciones si las inicializás cerca de  . Creo que eso puede ayudar a entender un poco mejor.
. Creo que eso puede ayudar a entender un poco mejor.
No, no es un si y sólo si. Podés tener convergencia incluso si
 , pero si
, pero si  no podés garantizar la convergencia.
no podés garantizar la convergencia.Un par de ejemplos sencillos es aproximar la raíz
 para las iteraciones
para las iteraciones  y
y  . En ambos casos tenés
. En ambos casos tenés  , pero en uno la derivada es menor a 1 en un entorno de
, pero en uno la derivada es menor a 1 en un entorno de  y en el otro es mayor. Probá (implementando) qué pasa con esas iteraciones si las inicializás cerca de
y en el otro es mayor. Probá (implementando) qué pasa con esas iteraciones si las inicializás cerca de  . Creo que eso puede ayudar a entender un poco mejor.
. Creo que eso puede ayudar a entender un poco mejor.Gracias. Entiendo que cuando es igual a 1 no se puede asegurar nada, pero en el mensaje anterior pusiste que si |g'(x*)|>1 entonces no converge, eso si se cumple?
Hola, a lo mejor ayuda ponerlo de esta manera:
Si  es continua y
es continua y  , por continuidad va a haber un entorno de
, por continuidad va a haber un entorno de  en donde
en donde  . En este caso la función
. En este caso la función  es contractiva en ese entorno, y por lo tanto para los
es contractiva en ese entorno, y por lo tanto para los  en ese entorno se tiene
en ese entorno se tiene  . Es decir las sucesivas aplicaciones de
. Es decir las sucesivas aplicaciones de  acercan los puntos del entorno al punto fijo. Por eso converge el MIG.
acercan los puntos del entorno al punto fijo. Por eso converge el MIG.
 es continua y
es continua y  , por continuidad va a haber un entorno de
, por continuidad va a haber un entorno de  en donde
en donde  . En este caso la función
. En este caso la función  es contractiva en ese entorno, y por lo tanto para los
es contractiva en ese entorno, y por lo tanto para los  en ese entorno se tiene
en ese entorno se tiene  . Es decir las sucesivas aplicaciones de
. Es decir las sucesivas aplicaciones de  acercan los puntos del entorno al punto fijo. Por eso converge el MIG.
acercan los puntos del entorno al punto fijo. Por eso converge el MIG.Si  es continua y
es continua y  , por continuidad va a haber un entorno de
, por continuidad va a haber un entorno de  en donde
en donde  . En este caso la función
. En este caso la función  es expansiva en ese entorno, y por lo tanto para los
es expansiva en ese entorno, y por lo tanto para los  en ese entorno se tiene
en ese entorno se tiene  . Es decir las sucesivas aplicaciones de
. Es decir las sucesivas aplicaciones de  alejan los puntos del entorno del punto fijo. Por ese diverge el MIG.
alejan los puntos del entorno del punto fijo. Por ese diverge el MIG.
 es continua y
es continua y  , por continuidad va a haber un entorno de
, por continuidad va a haber un entorno de  en donde
en donde  . En este caso la función
. En este caso la función  es expansiva en ese entorno, y por lo tanto para los
es expansiva en ese entorno, y por lo tanto para los  en ese entorno se tiene
en ese entorno se tiene  . Es decir las sucesivas aplicaciones de
. Es decir las sucesivas aplicaciones de  alejan los puntos del entorno del punto fijo. Por ese diverge el MIG.
alejan los puntos del entorno del punto fijo. Por ese diverge el MIG.Si  , entonces hay que ver bien el entorno para ver si en el entorno del punto fijo la función
, entonces hay que ver bien el entorno para ver si en el entorno del punto fijo la función  es contractiva o expansiva (por ejemplo, si es
es contractiva o expansiva (por ejemplo, si es  es suficientemente suave podés tomar las siguientes derivadas para analizar el comportamiento en el entorno, considerando que quisieras que la derivada primera tendiera a decrecer en su entorno).
es suficientemente suave podés tomar las siguientes derivadas para analizar el comportamiento en el entorno, considerando que quisieras que la derivada primera tendiera a decrecer en su entorno).
Por las dudas, para ser más exhaustivo: si en todo un entorno de
en todo un entorno de  entonces
entonces  es casi seguramente igual a la función identidad en ese entorno, y por lo tanto las sucesivas iteraciones no mueven el punto de iteración, es decir no converge.
es casi seguramente igual a la función identidad en ese entorno, y por lo tanto las sucesivas iteraciones no mueven el punto de iteración, es decir no converge.
 , entonces hay que ver bien el entorno para ver si en el entorno del punto fijo la función
, entonces hay que ver bien el entorno para ver si en el entorno del punto fijo la función  es contractiva o expansiva (por ejemplo, si es
es contractiva o expansiva (por ejemplo, si es  es suficientemente suave podés tomar las siguientes derivadas para analizar el comportamiento en el entorno, considerando que quisieras que la derivada primera tendiera a decrecer en su entorno).
es suficientemente suave podés tomar las siguientes derivadas para analizar el comportamiento en el entorno, considerando que quisieras que la derivada primera tendiera a decrecer en su entorno).Por las dudas, para ser más exhaustivo: si
 en todo un entorno de
en todo un entorno de  entonces
entonces  es casi seguramente igual a la función identidad en ese entorno, y por lo tanto las sucesivas iteraciones no mueven el punto de iteración, es decir no converge.
es casi seguramente igual a la función identidad en ese entorno, y por lo tanto las sucesivas iteraciones no mueven el punto de iteración, es decir no converge.
Saludos.
En respuesta a Juan Manuel Rivara De Leon
Re: Convergencia de un MIG
Se entendió perfecto. Muchas gracias!!
Hola,
A lo que dice Juan Manuel (que comparto) agrego un comentario. Si mirás la demostración del Teorema 4.7.4 de las notas, la cuenta que se hace (para el recíproco y poniendo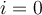 ) funciona independientemente de si
) funciona independientemente de si  es mayor o menor que
es mayor o menor que  . Lo que pasa es que si es mayor a
. Lo que pasa es que si es mayor a  , te termina quedando que si
, te termina quedando que si  estuviera cerca de
estuviera cerca de  , entonces el cociente
, entonces el cociente  sería mayor a
sería mayor a  , lo que implica que los iterados se estarían alejando de
, lo que implica que los iterados se estarían alejando de  .
.
Aprovecho también a aclarar por qué no ponemos un resultado de no-convergencia. Por más que , si justo te pasa que
, si justo te pasa que  entonces vas a tener convergencia: te queda
entonces vas a tener convergencia: te queda  para todo
para todo  . Puede pasar que
. Puede pasar que  esté lejos de
esté lejos de  y que pase eso.
y que pase eso.
Como estamos trabajando con lápiz y papel, no tenemos problemas de representación de números ni para evaluar . Ahora, esto es como dejar parado un huevo: puede pasar, pero en la práctica cualquier perturbación te lo va a hacer caer. Al trabajar con punto flotante, lo esperable (salvo que
. Ahora, esto es como dejar parado un huevo: puede pasar, pero en la práctica cualquier perturbación te lo va a hacer caer. Al trabajar con punto flotante, lo esperable (salvo que  sea representable exactamente) es que tengas algún errorcito de representación al escribir
sea representable exactamente) es que tengas algún errorcito de representación al escribir  . Si
. Si  , entonces el argumento de Juan Manuel aplica y lo que vas a observar es que
, entonces el argumento de Juan Manuel aplica y lo que vas a observar es que  se aleja de
se aleja de  .
.
Por eso decimos que si es "esperable" que el MIG no converja (y en la práctica no va a converger salvo algún caso patológico), pero no podemos asegurar (escribir en forma de teorema) la no-convergencia.
es "esperable" que el MIG no converja (y en la práctica no va a converger salvo algún caso patológico), pero no podemos asegurar (escribir en forma de teorema) la no-convergencia.
A lo que dice Juan Manuel (que comparto) agrego un comentario. Si mirás la demostración del Teorema 4.7.4 de las notas, la cuenta que se hace (para el recíproco y poniendo
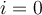 ) funciona independientemente de si
) funciona independientemente de si  es mayor o menor que
es mayor o menor que  . Lo que pasa es que si es mayor a
. Lo que pasa es que si es mayor a  , te termina quedando que si
, te termina quedando que si  estuviera cerca de
estuviera cerca de  , entonces el cociente
, entonces el cociente  sería mayor a
sería mayor a  , lo que implica que los iterados se estarían alejando de
, lo que implica que los iterados se estarían alejando de  .
.Aprovecho también a aclarar por qué no ponemos un resultado de no-convergencia. Por más que
 , si justo te pasa que
, si justo te pasa que  entonces vas a tener convergencia: te queda
entonces vas a tener convergencia: te queda  para todo
para todo  . Puede pasar que
. Puede pasar que  esté lejos de
esté lejos de  y que pase eso.
y que pase eso.Como estamos trabajando con lápiz y papel, no tenemos problemas de representación de números ni para evaluar
 . Ahora, esto es como dejar parado un huevo: puede pasar, pero en la práctica cualquier perturbación te lo va a hacer caer. Al trabajar con punto flotante, lo esperable (salvo que
. Ahora, esto es como dejar parado un huevo: puede pasar, pero en la práctica cualquier perturbación te lo va a hacer caer. Al trabajar con punto flotante, lo esperable (salvo que  sea representable exactamente) es que tengas algún errorcito de representación al escribir
sea representable exactamente) es que tengas algún errorcito de representación al escribir  . Si
. Si  , entonces el argumento de Juan Manuel aplica y lo que vas a observar es que
, entonces el argumento de Juan Manuel aplica y lo que vas a observar es que  se aleja de
se aleja de  .
.Por eso decimos que si
 es "esperable" que el MIG no converja (y en la práctica no va a converger salvo algún caso patológico), pero no podemos asegurar (escribir en forma de teorema) la no-convergencia.
es "esperable" que el MIG no converja (y en la práctica no va a converger salvo algún caso patológico), pero no podemos asegurar (escribir en forma de teorema) la no-convergencia.