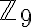Tengo una duda al respecto, es sobre que en realidad se podían considerar dos conjuntos (Z9,×) y (Z9,+), siendo el primero el que da un total de 0 homomorfismos de grupo, dado él que no es uno. Está este razonamiento bien? Cómo podía asumir cuál conjunto usar?
En particular, tomé el multiplicativo y me dio 0. Al ver las respuestas me di cuenta que debería haber asumido el otro caso, cómo?
El conjunto 
, con la operación producto de clases de equivalencia, no forma un grupo. Por ejemplo, la clase asociada al 0 no tiene inverso. Esa es la razón por la cual no tiene sentido considerar con la operación producto. Cuando hablamos del grupo , sin mencionar la operación
asociada, se sobre-entiende que la operación es la suma usual de clases
de equivalencia.
Por otro lado, se preguntaba por la cantidad de homomorfismos, no por la cantidad de homomorfismos no triviales. Por lo tanto la respuesta no podía ser cero, dado que el homomorfismo trivial siempre existe entre dos grupos.
Saludos.