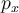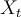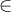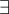Consultas Teórico/Práctico

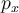
Luego bueno, para codificar una instancia de SOLITARE, primero veo que una instancia se puede ver como una 4-upla $(p_x,p_o,n,m)$ donde $p_x$ son las posiciones donde hay un X, $p_o$ posiciones donde hay un O.

Luego para la instancia la represento mediante dos matrices X, O donde si X[i,j] = 1, entonces en (i,j) hay una X, caso contrario X[i,j] = 0, en (i,j) no hay una X, analogo para O.

Formar una codificacion s a partir de esto se puede hacer concatenando las filas de X y O que son 1's y 0's y a este codigo concatenarle la expresion binaria de m y n, ademas de concatenar otro codigo para determinar la cantidad de bits a representar m,n. Es facil ver que en esta representacion |s| = O(mn).

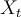
Luego, para representar un certificado que lo consideramos como un par ($p_xt$,$p_yt$) de posiciones, simplemente lo damos como dos matrices de bits $X_t$ y $O_t$. el codigo t lo obtenemos concatenando las filas de ambas matrices, y vemos que |t| = O(mn) = O(|s|).

Luego un B certificador eficiente cumple que:
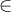
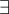
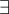
1- s $\in$ SOLITARE $\Longleftrightarrow$ ($\exists$ t) B(s,t) = yes ( la condicion |t| $\leqslant$ p(|s|), como |t| = O(|s|) entonces  ($\exists$  c > 0) |t|  $\leqslant$  c|s|, por tanto con el polinomio p(x) = x*c se verifica)
2- B es polinomial respecto a |s| + |t| (como |t| = O(|s|) en realidad es suficiente con verificar que es polinomial respecto a |s|)

luego ahora damos el certificado, y voy a verificar solo la segunda condición, la primera que es el sii no es difícil de probar y es larga y no me gustaría explayarme tanto.

El algoritmo certificador B es el siguiente:

0- El algoritmo en vez de estar especificado respecto a las posiciones, están especificado respecto a las matrices que representan a la listas de posiciones, capaz no es lo mas correcto, pero ayuda en la visualización para determinar el orden de complejidad (no se si esto es un problema o seria mejor hacerlo con el conjunto de posiciones al algoritmo en alto nivel, en tal caso justificar el orden se complica.)

1- Se verifica que tanto (X, O) como $(X_t, O_t)$ no se solapen, esto es, que no exista (i,j) tal que (X[i,j] = O[i,j] = 1 || X_t[i,j] = O_t[i,j] = 1), en caso que se cumpla esta ultima expresión lógica para algún par (i,j), el algoritmo retorna NO y termina.

2- Se verifica que $(X_t, O_t)$ sea subconjunto de fichas de (X,O), esto es, que la expresión lógica ( $X_t$[i,j] = 1 && X[i,j] = 0 ||  $O_t$[i,j] = 1 && O[i,j] = 0) no se cumpla para algún par (i,j), en caso de cumplirse para alguno, retorno NO y termino.

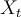
3- Se verifica que las fichas de toda fila sean del mismo tipo, esto se hace facilmente verificando que la expresion ( $X_t$[i, $j_1$] = 1 && $O_t$[i, $j_2$] = 1 ) no se cumpla para alguna terna $(i,j_1,j_2)$, en caso de cumplirse, retorno NO y termino.

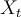
4- Se verifica que toda columna tenga algún símbolo, verificando que la expresión ($X_t$[$i_1$,j] = 1 || $O_t$[$i_2$,j] = 1) se cumpla para todo j con algún par $(i_1,i_2)$, caso contrario, se retorna NO y termino.

5- finalmente si no termine en ningún paso previo, retorno SI y termino.

Luego es fácil ver que en este algoritmo se hacen simplemente recorridas sobre las matrices, por tanto es O(mn), que cumple con ser polinomial en |s|.

Termino preguntando si el algoritmo dado lo consideran lo suficientemente aceptable para el curso, en vez de escribir fors y whiles, creo que es mas compacto y refleja bien lo que hay que hacer en cada paso. También, esta bien la forma en que codifique las entradas y los t? y las simplificaciones que hice en la definición de B sabiendo que |t| era O(|s|) ?