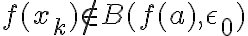Teorema 5.9 Notas del Curso

Teorema 5.9 Notas del Curso

de Alexis Sokorov Vargas -
Número de respuestas: 1

Buenas tardes, tengo una pequeña duda respecto a esta parte de la demostración:


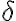Cuando se hace uso de la NO continuidad de f en a se toman \delta cada vez más chicos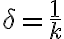 \delta = \frac{1}{k} 

No entiendo el espíritu de hacer eso, es decir, ¿cómo sé que, tomándome 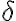\delta cada vez más chicos , me aseguro de que se cumple que mi función no logre ser continua?

¿Cómo sé que  \exists  x_k \in B(a, \delta _{k} ) \cap D cuya imagen f(x_{k}) \notin B(f(a), \epsilon _{0}) ?
En respuesta a Alexis Sokorov Vargas

Re: Teorema 5.9 Notas del Curso

de Marcelo Fiori -
Hola Alexis,
estamos suponiendo que la función no es continua, y por lo tanto estamos usando que para todo \delta pasa tal cosa. Es decir, no estamos probando que no es continua con esos delta, sino que estamos usando que, si f no es continua, entonces para cada \delta podemos hacer tal cosa, y con eso llegamos a una contradicción con las hipótesis (que proviene de suponer que la función no era continua)
Saludos!