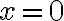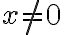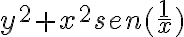CDIVV-2S: Segundo Parcial (2018, ejercicio 3)

Buenas tardes, tengo un par de dudas respecto a este ejercicio:

Primero traté de ver la continuidad de la función en el $(0,0)$ y llegué a que no lo es. Entonces puedo concluir que ya no es diferenciable porque no se cumple ese primer ítem.

Proseguí con sus derivadas parciales y lo planteé de una forma que no estoy muy convencido:

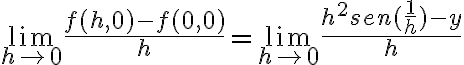$\lim_{h \to 0} \frac{ f(h,0) - f(0,0) }{h} = \lim_{h \to 0} \frac{ h^2 sen ( \frac{1}{h} ) - y}{h}$ y ese límite me da que no existe. Entonces me descarto la existencia de derivadas parciales. Llegaría a la opción 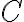$C$ pero no sé si es por ahí la mano

Re: Segundo Parcial (2018, ejercicio 3)

de Leandro Bentancur - domingo, 19 de noviembre de 2023, 18:22

Buenas tardes Alexis,
Hay un problema allí y es que

$y$ es una variable, no una constante, por lo tanto al evaluarla en

$(0,0)$ su valor resulta

$0$ . Por ejemplo para la continuidad, si nos acercamos al

$(0,0)$ por puntos de la recta

$x=0$ entonces la función vale

$y$ y el límite es

$0$ , y luego si nos acercamos por puntos fuera de la recta (puntos tq

$x \neq 0$ ) entonces la función vale

$y^2 + x^2 sen(\frac{1}{x})$ que por tu argumento vale también

$0$ , por lo tanto la función es continua en el origen.
Saludos,
Leandro