Buen día, Diego.
Siguiendo la demostración de Lagrange, asumiendo que tenemos un homomorfismo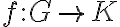 con
con 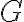 un grupo finito, tenemos que
un grupo finito, tenemos que 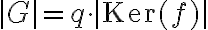 , donde
, donde  es la cantidad de clases de equivalencia de cierta relación. Concretamente, la relación está dada por
es la cantidad de clases de equivalencia de cierta relación. Concretamente, la relación está dada por 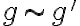 si y solamente si
si y solamente si 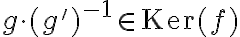 . Entonces, la demostración del teorema de los órdenes se reduce a demostrar que
. Entonces, la demostración del teorema de los órdenes se reduce a demostrar que  coincide con la cardinalidad de la imagen de
coincide con la cardinalidad de la imagen de  . Lo anterior se logra construyendo una biyección entre la imagen de
. Lo anterior se logra construyendo una biyección entre la imagen de  y otro conjunto con cardinalidad
y otro conjunto con cardinalidad  , a saber, el conjunto formado por todas las clases de equivalencia de la relación
, a saber, el conjunto formado por todas las clases de equivalencia de la relación 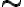 .
.
Para construir la biyección mencionada, hay que tener en cuenta lo que mencionas de que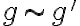 si y solamente si,
si y solamente si, 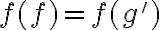 . Podemos definir
. Podemos definir 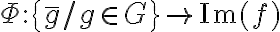 como
como 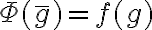 , donde
, donde 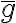 denota la clase de equivalencia de
denota la clase de equivalencia de  . Primero hay que ver que
. Primero hay que ver que 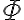 está bien definida, es decir, que
está bien definida, es decir, que 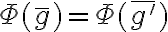 si
si 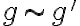 . Esto es claro ya que
. Esto es claro ya que 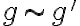 si y solamente si
si y solamente si 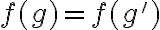 . La definición de
. La definición de 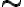 también se puede usar para demostrar la inyectividad de
también se puede usar para demostrar la inyectividad de 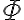 , es decir,
, es decir, 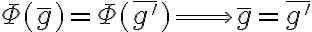 . Finalmente, si tomas
. Finalmente, si tomas 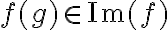 , vamos a tener que
, vamos a tener que 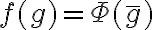 por definición de
por definición de 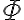 , es decir,
, es decir, 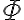 es sobreyectiva. Al ser entonces
es sobreyectiva. Al ser entonces 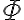 una biyección, vas a tener que
una biyección, vas a tener que 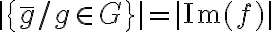 , es decir,
, es decir, 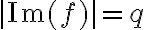 .
.
Espero que lo anterior sea de ayuda.
Por cierto, hay una demostración más sencilla del teorema de los órdenes, que es un corolario del primer teorema de isomorfismos. Está en las notas que subí la semana pasada.
Saludos cordiales,
Marco
Siguiendo la demostración de Lagrange, asumiendo que tenemos un homomorfismo
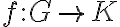 con
con 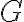 un grupo finito, tenemos que
un grupo finito, tenemos que 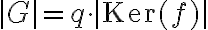 , donde
, donde  es la cantidad de clases de equivalencia de cierta relación. Concretamente, la relación está dada por
es la cantidad de clases de equivalencia de cierta relación. Concretamente, la relación está dada por 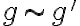 si y solamente si
si y solamente si 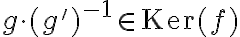 . Entonces, la demostración del teorema de los órdenes se reduce a demostrar que
. Entonces, la demostración del teorema de los órdenes se reduce a demostrar que  coincide con la cardinalidad de la imagen de
coincide con la cardinalidad de la imagen de  . Lo anterior se logra construyendo una biyección entre la imagen de
. Lo anterior se logra construyendo una biyección entre la imagen de  y otro conjunto con cardinalidad
y otro conjunto con cardinalidad  , a saber, el conjunto formado por todas las clases de equivalencia de la relación
, a saber, el conjunto formado por todas las clases de equivalencia de la relación 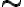 .
. Para construir la biyección mencionada, hay que tener en cuenta lo que mencionas de que
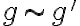 si y solamente si,
si y solamente si, 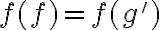 . Podemos definir
. Podemos definir 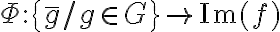 como
como 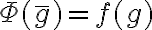 , donde
, donde 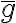 denota la clase de equivalencia de
denota la clase de equivalencia de  . Primero hay que ver que
. Primero hay que ver que 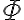 está bien definida, es decir, que
está bien definida, es decir, que 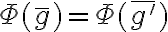 si
si 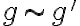 . Esto es claro ya que
. Esto es claro ya que 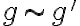 si y solamente si
si y solamente si 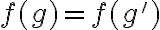 . La definición de
. La definición de 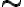 también se puede usar para demostrar la inyectividad de
también se puede usar para demostrar la inyectividad de 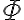 , es decir,
, es decir, 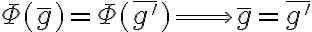 . Finalmente, si tomas
. Finalmente, si tomas 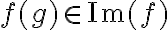 , vamos a tener que
, vamos a tener que 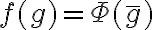 por definición de
por definición de 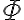 , es decir,
, es decir, 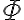 es sobreyectiva. Al ser entonces
es sobreyectiva. Al ser entonces 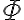 una biyección, vas a tener que
una biyección, vas a tener que 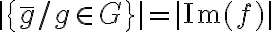 , es decir,
, es decir, 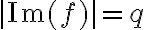 .
. Espero que lo anterior sea de ayuda.
Por cierto, hay una demostración más sencilla del teorema de los órdenes, que es un corolario del primer teorema de isomorfismos. Está en las notas que subí la semana pasada.
Saludos cordiales,
Marco
