Hola Alexis,
que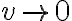
es relativamente sencillo de ver. Fijate de la definición que 
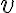tiene dos sumandos. El primero es una transformación lineal evaluada en 
. Las T.L. en cero valen cero, por definición, y son continuas como funciones, así que tenemos que ese primer término tiende a cero. El segundo es un resto, que tiende a cero (incluso más rápido que la norma de , pero eso no lo necesitamos en este momento).
Para ver que el otro término está acotado podés usar la desigualdad triangular. El segundo sumando que sale de ahí es el resto (ahora sí hay que usar la propiedad completa del resto), y el primero es una T.L. evaluada en h, sobre la norma de h. Si querés podés pensar a la T.L. como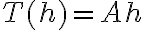
, con alguna matriz asociada (que en este caso es la Jacobiana), entonces cuando dividís entre la norma de h te queda la T.L. evaluada en un vector de norma uno.
Saludos!
que
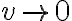es relativamente sencillo de ver. Fijate de la definición que 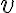tiene dos sumandos. El primero es una transformación lineal evaluada en . Las T.L. en cero valen cero, por definición, y son continuas como funciones, así que tenemos que ese primer término tiende a cero. El segundo es un resto, que tiende a cero (incluso más rápido que la norma de , pero eso no lo necesitamos en este momento).Para ver que el otro término está acotado podés usar la desigualdad triangular. El segundo sumando que sale de ahí es el resto (ahora sí hay que usar la propiedad completa del resto), y el primero es una T.L. evaluada en h, sobre la norma de h. Si querés podés pensar a la T.L. como
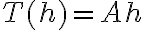, con alguna matriz asociada (que en este caso es la Jacobiana), entonces cuando dividís entre la norma de h te queda la T.L. evaluada en un vector de norma uno.Saludos!