En el teórico de esta semana trabajaremos con el tema Diferenciabilidad. Las clases de OpenFING para el teórico de esta semana son:
- Clase 27: Se comenzará revisitando el tema derivada de funciones de una variable desde el lenguaje de la diferenciabilidad. Luego, se verá la definición de diferenciabilidad de una función de en
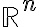, y en 
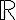en particular el casod e 
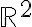. También se verá el teorema que dice que diferenciabilidad implica continuidad y existencia de derivadas parciales, y derivadas direccionales. Se verá la definición de gradiente, y sus interpretaciones como dirección de máximo crecimiento, y tangente a curvas de nivel. Por último se verá un ejemplo donde se prueba la diferenciabilidad de una función a partir de la definición. - Clase 30 (edición 2018): Se verá la definición de plano tangente y más ejemplos de diferenciabilidad a partir de la definición. Por último se verá la condición suficiente de diferenciabilidad en términos de las derivadas parciales (con demostración).
Clase 29: Se vará enunciado y demostración de Regla de la cadena (I) y el enunciado de la Regla de la cadena (II), asi como varios ejemplos.
Durante la primer clase de esta semana deberán trabajar con el séptimo repartido de práctico, y durante la segunda con el octavo repartido de práctico. Les recordamos que hay disponibles un video de introducción al práctico 7 y un video de introducción al práctico 8. Además hay dos videos muy buenos realizados por la profesora Matilde Martínez:
- Funciones de dos variables, cómo se grafican y noción de continuidad.
- Qué es la diferenciabilidad y porqué se define así?
Está disponible también, el cuestionario de auto-evaluación sobre límites, continuidad y derivadas parciales para que lo realicen cuando lo consideren oportuno.
La guía bibliográfica para esta semana serán las Notas del Curso (páginas 97 a 108).
Buen trabajo!