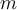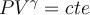F2 - 2S: 6.4

Hola, tengo un par de preguntas.

En este ejercicio es correcta la siguiente igualdad de energías?

Es decir, ¿la suma de la energía cinética de la masa más la energía interna del gas (condiciones iniciales) es igual a la energía interna final del gas (condiciones finales)?

Intenté resolver el ejercicio con esa ecuación y además sabiendo que $PiVi^λ = PfVf^λ$ por ser adiabático, pero no logré llegar al resultado.

Por otro lado, en la primera ecuación que puse puedo sustituir $nRTi$ por $PiVi$ y $nRTf$ por $PfVf$ ? O en este caso no se cumple porque el aire no es un gas ideal?

Gracias!

Re: 6.4

de Virginia Feldman - miércoles, 11 de octubre de 2023, 17:02

Hola.
La ecuación inicial es correcta. Podemos pensar de dónde sale para asegurarnos de que está bien. Si tomamos al gas como nuestro sistema, este sigue un proceso adiabático, por lo tanto Q=0 y, por la primera ley

$W_{sobregas}=\Delta U=nc_v(T_f-T_i)$ . Por otro lado, si estudiamos el sistema correspondiente a la masa

$m$ se tiene que el trabajo realizado sobre ella debe ser igual al cambio en su energía cinética:

$W_{porgas}=-W_{sobregas}=\Delta K=-\frac{1}{2}mv_i^2$ . De donde se puede despejar tu primera ecuación.
Después, como bien decís, se puede usar la relación para procesos adiabáticos cuasiestáticos:

$PV^\gamma=cte$ , aplicándola a los estados inicial y final del gas.
La ecuación de estado del gas ideal se puede aplicar en este caso, porque suponemos que el aire se comporta como un gas ideal, como dice la letra.
Así que el razonamiento es correcto, revisá las cuentas que puede haber un error ahí.
Saludos.