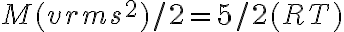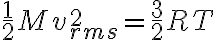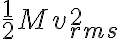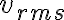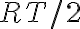Buenas!
En este ejercicio use la siguiente ecuación:
de la cual despeje M con los datos 300K y 1920m/s. Luego, ese mismo M lo use para hallar vrms que pide la letra.
El resultado me dio bien, pero mi pregunta es acerca de la ecuación en sí.
Ese valor M es la masa molar del H2? Pregunto ya que mi primer instinto fue buscar la masa molar del H2 en internet, pero no me da lo mismo que al calcularla con esa ecuación. No entiendo cual es la diferencia entre ambos valores o si me estoy confundiendo de términos. Gracias!