Buenas Estudiantes,
A continuación van algunas sugerencias para abordar los 13 ejercicios de la lista.
Ejercicio 1) Este es un resultado clásico sobre matrices totalmente unimodulares. Se puede demostrar empleando el principio de inducción completa sobre el tamaño de la submatriz cuadrada.
Ejercicio 2) Aplicar el algoritmo sugerido en la última diapositiva de la clase 3 a una instancia cualquiera 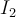 del problema
del problema  y utilizar las hipótesis.
y utilizar las hipótesis.
Ejercicios 3 y 4) Seguir las sugerencias indicadas en la clase 5.
Ejercicio 5) Traducir los problemas descriptos al MST cuando  , o al problema de Steiner cuando
, o al problema de Steiner cuando  .
.
Ejercicio 6) Leer el artículo sobre la Historia del Problema de Steiner Euclídeo disponible aquí.
Ejercicio 7) Dado un grafo 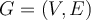 , el MAX-
, el MAX-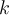 -CUT consiste en encontrar la partición de vértices
-CUT consiste en encontrar la partición de vértices  que tiene la máxima cantidad de aristas en
que tiene la máxima cantidad de aristas en 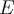 con un extremo en algún
con un extremo en algún 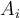 y un extremo en algún
y un extremo en algún  tal que
tal que 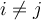 . Se recomienda seleccionar inicialmente
. Se recomienda seleccionar inicialmente 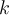 vértices cualesquiera
vértices cualesquiera  de
de  , definir inicialmente
, definir inicialmente  para cada
para cada  y luego agregar de manera golosa a todos los restantes vértices de
y luego agregar de manera golosa a todos los restantes vértices de  .
.
Ejercicio 8) Formular el problema primal siguiendo el Ejercicio 12.10 del libro de Vazirani. Sea  el conjunto de aristas que elige Kruskal con costos
el conjunto de aristas que elige Kruskal con costos  y sea
y sea  . Notar que
. Notar que  .
.
Mostrar que la tupla  dada por
dada por  para cada
para cada  , mientras que
, mientras que  o
o  para cualquier otro subconjunto
para cualquier otro subconjunto 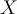 de
de 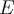 es solución factible dual. Utilizar esta solución para resolver el ejercicio empleando resultados de dualidad.
es solución factible dual. Utilizar esta solución para resolver el ejercicio empleando resultados de dualidad.
Ejercicio 9) Seguir las sugerencias del Ejercicio 12.11 del libro de Vazirani.
Ejercicio 10) Recordar la existencia de algoritmos de aproximación para el problema de Redes de Steiner.
Ejercicio 11: En el libro de Vazirani se detalla una formulación del problema de cubrimiento de vértices de mínimo peso como problema de programación lineal entera. Duplicar la solución óptima del problema relajado.
Ejercicio 12: Probar primero existencia de alguna solución. Luego, mostrar que si dos coordenadas de
 no son idénticas entonces
no son idénticas entonces 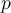 no alcanza el máximo.
no alcanza el máximo.
Ejercicio 13: Aplicar directamente la definición de supermodularidad débil.
Cordiales saludos,
Pablo.