Hola, Ezequiel.
Ya lo tienes prácticamente hecho.
Faltaría justificar que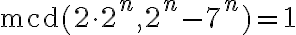 , pero esto es cierto ya que el único factor primo de
, pero esto es cierto ya que el único factor primo de 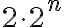 es 2, mientras que
es 2, mientras que 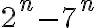 siempre es impar. Por lo tanto,
siempre es impar. Por lo tanto, 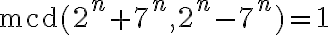 , y ya estaría. Otra forma de hacerlo es resolviendo la ecuación diofántica, como propones. Pero me parece que por este camino se complica bastante. Respecto a tu pregunta, sí, las soluciones están en función de cada
, y ya estaría. Otra forma de hacerlo es resolviendo la ecuación diofántica, como propones. Pero me parece que por este camino se complica bastante. Respecto a tu pregunta, sí, las soluciones están en función de cada  . Fíjate que para
. Fíjate que para 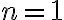 , te queda la ecuación
, te queda la ecuación 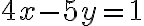 , que tiene solución
, que tiene solución 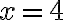 e
e 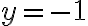 . Sin embargo, este par
. Sin embargo, este par 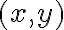 no es solución de
no es solución de 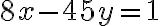 (la ecuación correspondiente a
(la ecuación correspondiente a 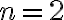 ).
).
Saludos,
Marco
Ya lo tienes prácticamente hecho.
Faltaría justificar que
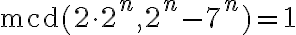 , pero esto es cierto ya que el único factor primo de
, pero esto es cierto ya que el único factor primo de 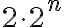 es 2, mientras que
es 2, mientras que 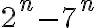 siempre es impar. Por lo tanto,
siempre es impar. Por lo tanto, 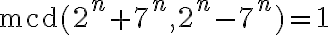 , y ya estaría. Otra forma de hacerlo es resolviendo la ecuación diofántica, como propones. Pero me parece que por este camino se complica bastante. Respecto a tu pregunta, sí, las soluciones están en función de cada
, y ya estaría. Otra forma de hacerlo es resolviendo la ecuación diofántica, como propones. Pero me parece que por este camino se complica bastante. Respecto a tu pregunta, sí, las soluciones están en función de cada  . Fíjate que para
. Fíjate que para 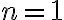 , te queda la ecuación
, te queda la ecuación 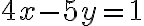 , que tiene solución
, que tiene solución 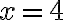 e
e 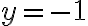 . Sin embargo, este par
. Sin embargo, este par 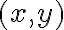 no es solución de
no es solución de 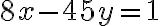 (la ecuación correspondiente a
(la ecuación correspondiente a 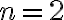 ).
).Saludos,
Marco
