Hola, Matías:
Lo primero que debes demostrar es que para cada número de la forma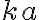 , con
, con 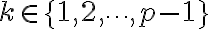 existe un resto
existe un resto 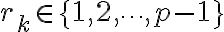 tal que
tal que 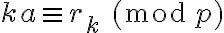 . Debes darte cuenta de cuál teorema visto en clases te garantiza la existencia de dicho resto
. Debes darte cuenta de cuál teorema visto en clases te garantiza la existencia de dicho resto 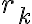 , y por otro lado, debes probar que
, y por otro lado, debes probar que 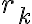 no puede ser cero (puedes acá emplear reducción al absurdo). Luego, debes demostrar que los
no puede ser cero (puedes acá emplear reducción al absurdo). Luego, debes demostrar que los 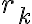 son distintos para cada
son distintos para cada 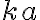 , es decir, que si
, es decir, que si 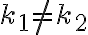 entonces
entonces 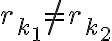 . Nuevamente, para esta parte te recomiendo que uses reducción al absurdo. Es muy importante también tener en cuenta la hipótesis de que
. Nuevamente, para esta parte te recomiendo que uses reducción al absurdo. Es muy importante también tener en cuenta la hipótesis de que 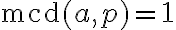 .
.
Para la parte que corresponde al Teorema de Fermat, tienes un post mío al respecto que hice el día de ayer.
Saludos,
Marco
Lo primero que debes demostrar es que para cada número de la forma
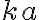 , con
, con 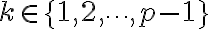 existe un resto
existe un resto 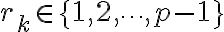 tal que
tal que 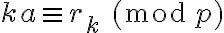 . Debes darte cuenta de cuál teorema visto en clases te garantiza la existencia de dicho resto
. Debes darte cuenta de cuál teorema visto en clases te garantiza la existencia de dicho resto 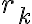 , y por otro lado, debes probar que
, y por otro lado, debes probar que 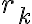 no puede ser cero (puedes acá emplear reducción al absurdo). Luego, debes demostrar que los
no puede ser cero (puedes acá emplear reducción al absurdo). Luego, debes demostrar que los 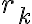 son distintos para cada
son distintos para cada 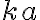 , es decir, que si
, es decir, que si 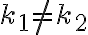 entonces
entonces 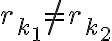 . Nuevamente, para esta parte te recomiendo que uses reducción al absurdo. Es muy importante también tener en cuenta la hipótesis de que
. Nuevamente, para esta parte te recomiendo que uses reducción al absurdo. Es muy importante también tener en cuenta la hipótesis de que 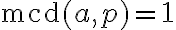 .
.Para la parte que corresponde al Teorema de Fermat, tienes un post mío al respecto que hice el día de ayer.
Saludos,
Marco
