buenas, quería preguntar de por qué se supone que en la solución dice que si alga es menor a menos uno, diverge, ya que tengo entendido que convergería a partir del menos uno.
Buenas,
Primero quería comentar que si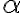 , hay que separar la integral como una integral de segunda especie en
, hay que separar la integral como una integral de segunda especie en  y otra de primera especie en
y otra de primera especie en 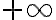 , esto es
, esto es 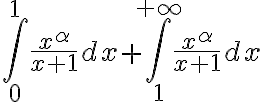 Vos estudiaste correctamente qué sucedía en infinito (hay un detalle ahí que es que la primera condición es
Vos estudiaste correctamente qué sucedía en infinito (hay un detalle ahí que es que la primera condición es 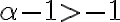 sii la integral converge y pusiste
sii la integral converge y pusiste  en lugar de
en lugar de 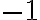 ). Tenemos entonces que la segunda integral converge si y sólo si
). Tenemos entonces que la segunda integral converge si y sólo si 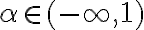 . Queda ver ahora cuando converge la primera e intersectar las condiciones.
. Queda ver ahora cuando converge la primera e intersectar las condiciones.
Saludos,
Leandro
Primero quería comentar que si
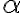 , hay que separar la integral como una integral de segunda especie en
, hay que separar la integral como una integral de segunda especie en  y otra de primera especie en
y otra de primera especie en 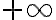 , esto es
, esto es 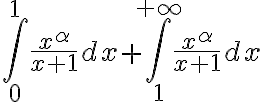 Vos estudiaste correctamente qué sucedía en infinito (hay un detalle ahí que es que la primera condición es
Vos estudiaste correctamente qué sucedía en infinito (hay un detalle ahí que es que la primera condición es 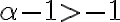 sii la integral converge y pusiste
sii la integral converge y pusiste  en lugar de
en lugar de 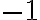 ). Tenemos entonces que la segunda integral converge si y sólo si
). Tenemos entonces que la segunda integral converge si y sólo si 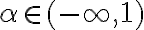 . Queda ver ahora cuando converge la primera e intersectar las condiciones.
. Queda ver ahora cuando converge la primera e intersectar las condiciones.Saludos,
Leandro
Perfecto, muchas gracias.
