Hola Alexis,
el (0,0) es punto de acumulación de A_5 porque, dada cualquier bola reducida de centro 0 y radio
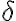
, se pueden encontrar puntos de A_5 que estén en esa bola.
Esto es porque como 1/n tiende a cero, dado un
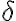
, vamos a poder encontrar un elemento de la forma (1/n,0) de forma tal que 1/n sea menor que ese
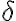
.
Recuerden que para ser punto de acumulación no nos importa si el punto en cuestión pertenece o no pertenece al conjunto (de hecho en la definición no aparece, porque tomamos bolas reducidas)
Por la misma razón que el párrafo anterior, el (0,0) es frontera de A_5. Los puntos frontera también pueden pertenecer o no al conjunto.
El resto de los puntos de A_5 también son frontera, porque dado cualquier entorno (¡no reducido ahora!) seguro que hay alguien del conjunto (el propio punto), y alguien del complemento (prácticamente todo el resto).
La clausura la definimos justamente como la unión del conjunto con su frontera (le unimos lo que le falta al conjunto para ser cerrado, básicamente). Así que eso es casi que por definición. Sin el casi.
Saludos!
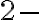 ¿Por qué el conjunto de puntos de acumulación es
¿Por qué el conjunto de puntos de acumulación es 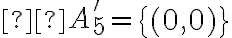 ?
?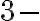 Por último, no me queda del todo el conjunto clausura de
Por último, no me queda del todo el conjunto clausura de  ,
, 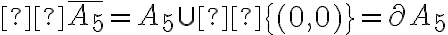
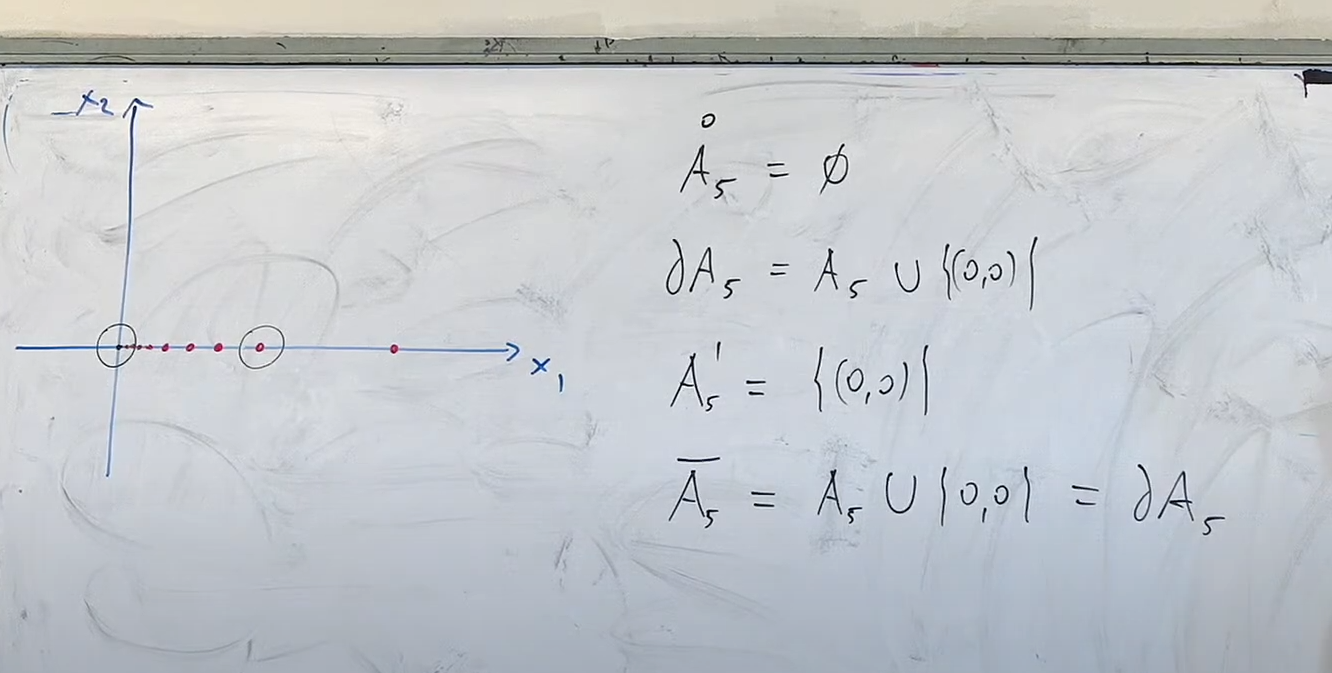
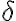 , se pueden encontrar puntos de A_5 que estén en esa bola.
, se pueden encontrar puntos de A_5 que estén en esa bola.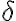 , vamos a poder encontrar un elemento de la forma (1/n,0) de forma tal que 1/n sea menor que ese
, vamos a poder encontrar un elemento de la forma (1/n,0) de forma tal que 1/n sea menor que ese 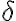 .
.