Hola buenas,
Me gustaria saber si esta demostracion es valida.
Lema.: Si 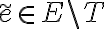 entonces
entonces 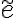 no pertenece a ningun MST de
no pertenece a ningun MST de 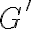
Demo.:
Si 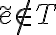 entonces
entonces  tiene un unico ciclo del que
tiene un unico ciclo del que  es la mas costosa, pues de no ser asi, si eliminaramos la mas costosa no habria ciclo en
es la mas costosa, pues de no ser asi, si eliminaramos la mas costosa no habria ciclo en 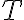 y por ende
y por ende 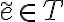 .
.
Como  es la arista mas costosa de un ciclo en un subgrafo de
es la arista mas costosa de un ciclo en un subgrafo de 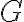 (
( ) lo es entonces tambien lo es del grafo completo
) lo es entonces tambien lo es del grafo completo 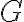 y como
y como 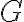 es un subgrafo de
es un subgrafo de 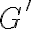 entonces
entonces  es la arista mas costosa de un ciclo en
es la arista mas costosa de un ciclo en 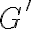 y por ende no pertenece a ningun MST de
y por ende no pertenece a ningun MST de 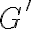 .
. 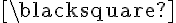
Como todo arbol tiene 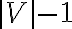 aristas tenemos que si existe otro arbol
aristas tenemos que si existe otro arbol 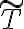 que sea MST y tenga una arista que no pertenece a
que sea MST y tenga una arista que no pertenece a 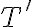 entonces este no tiene una arista
entonces este no tiene una arista 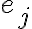 que pertenece a
que pertenece a 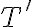 .
.
Sea 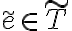 y
y 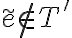
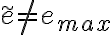 porque por 4.20 no pertenece a ningun MST.
porque por 4.20 no pertenece a ningun MST.
Caso 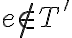 :
:
En este caso la nueva arista 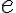 era la mas pesada del ciclo es decir
era la mas pesada del ciclo es decir 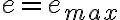 luego
luego 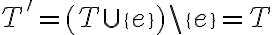 por lo que como
por lo que como 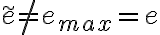 y
y 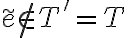 entonces
entonces 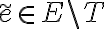 y por el lema es absurdo.
y por el lema es absurdo.
Caso 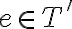 :
:
Como este caso no eliminamos 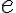 existe un
existe un 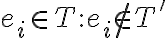
Luego sabemos que 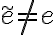 pues esta esta en
pues esta esta en 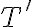 y ademas sabemos que
y ademas sabemos que 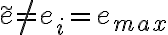
Por lo tanto como 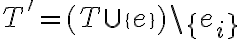 tenemos que los nodos que no estan en
tenemos que los nodos que no estan en 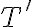 son
son 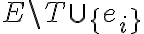 y como
y como 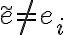 tenemos que
tenemos que 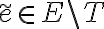 lo cual es absurdo por el lema.
lo cual es absurdo por el lema.
Por lo tanto es absurdo suponer que existe un MST de 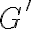 que difiera en una arista, consecuentemente todo MST de
que difiera en una arista, consecuentemente todo MST de 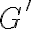 debe tener las mismas
debe tener las mismas 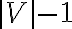 aristas que
aristas que 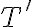 , por lo cual
, por lo cual 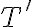 es MST de
es MST de 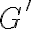 .
. 
Saludos,
Camilo.
En respuesta a Camilo Ferrero Alvarez
Re: Practico 6, ejercicio 3 parte a) ii)
de Fernando Fernandez -
Hola Camilo.
Está muy bien el lema. Y ahí ya casi tenías todo. El resto parece corresponder a un intento diferente de demostración, aunque parece correcto.
Con el lema habías descartado todas las aristas en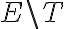 como posibles aristas de un MST de
como posibles aristas de un MST de 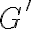 . Quedan como posibles candidatas las
. Quedan como posibles candidatas las  aristas de
aristas de 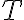 , y
, y 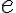 . Una de ellas es
. Una de ellas es 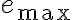 , que como explicás más abajo, y por la misma propiedad 4.20, tampoco puede pertenecer a un MST de
, que como explicás más abajo, y por la misma propiedad 4.20, tampoco puede pertenecer a un MST de 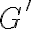 . Por lo tanto, las únicas posibles aristas de un MST son las
. Por lo tanto, las únicas posibles aristas de un MST son las  aristas en
aristas en 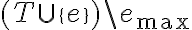 , y esto es
, y esto es 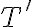 . Podrías agregar la demostración de que
. Podrías agregar la demostración de que 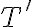 es un árbol (grafo conexo y acíclico) y que es de cubrimiento de
es un árbol (grafo conexo y acíclico) y que es de cubrimiento de 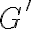 .
.
Algunos detalles.
Pusiste "todo árbol tiene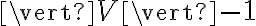 aristas". En realidad, un árbol puede tener menos aristas, incluso 0 (un árbol hoja). Debés haber querido poner árbol de cubrimiento. En esa misma frase, cuando ponés "este" me parece que querés decir
aristas". En realidad, un árbol puede tener menos aristas, incluso 0 (un árbol hoja). Debés haber querido poner árbol de cubrimiento. En esa misma frase, cuando ponés "este" me parece que querés decir 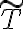 . Pero en realidad, por como está redactado, "este" sería
. Pero en realidad, por como está redactado, "este" sería 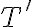 . Te sugiero que en lo posible evites los "este", "ese", "aquel", etc. De todas formas no parece que hagas uso de esa afirmación.
. Te sugiero que en lo posible evites los "este", "ese", "aquel", etc. De todas formas no parece que hagas uso de esa afirmación.
Más abajo donde dice "los nodos que no están en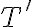 " seguramente quisiste decir "las aristas".
" seguramente quisiste decir "las aristas".
Está muy bien el lema. Y ahí ya casi tenías todo. El resto parece corresponder a un intento diferente de demostración, aunque parece correcto.
Con el lema habías descartado todas las aristas en
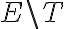 como posibles aristas de un MST de
como posibles aristas de un MST de 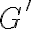 . Quedan como posibles candidatas las
. Quedan como posibles candidatas las  aristas de
aristas de 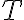 , y
, y 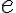 . Una de ellas es
. Una de ellas es 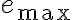 , que como explicás más abajo, y por la misma propiedad 4.20, tampoco puede pertenecer a un MST de
, que como explicás más abajo, y por la misma propiedad 4.20, tampoco puede pertenecer a un MST de 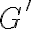 . Por lo tanto, las únicas posibles aristas de un MST son las
. Por lo tanto, las únicas posibles aristas de un MST son las  aristas en
aristas en 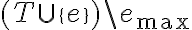 , y esto es
, y esto es 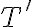 . Podrías agregar la demostración de que
. Podrías agregar la demostración de que 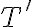 es un árbol (grafo conexo y acíclico) y que es de cubrimiento de
es un árbol (grafo conexo y acíclico) y que es de cubrimiento de 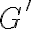 .
.Algunos detalles.
Pusiste "todo árbol tiene
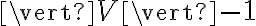 aristas". En realidad, un árbol puede tener menos aristas, incluso 0 (un árbol hoja). Debés haber querido poner árbol de cubrimiento. En esa misma frase, cuando ponés "este" me parece que querés decir
aristas". En realidad, un árbol puede tener menos aristas, incluso 0 (un árbol hoja). Debés haber querido poner árbol de cubrimiento. En esa misma frase, cuando ponés "este" me parece que querés decir 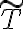 . Pero en realidad, por como está redactado, "este" sería
. Pero en realidad, por como está redactado, "este" sería 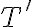 . Te sugiero que en lo posible evites los "este", "ese", "aquel", etc. De todas formas no parece que hagas uso de esa afirmación.
. Te sugiero que en lo posible evites los "este", "ese", "aquel", etc. De todas formas no parece que hagas uso de esa afirmación.Más abajo donde dice "los nodos que no están en
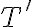 " seguramente quisiste decir "las aristas".
" seguramente quisiste decir "las aristas".