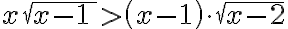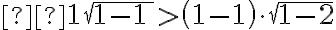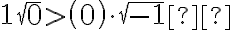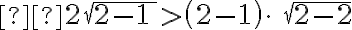Consulta ejercicio 13a Practico 1

Re: Consulta ejercicio 13a Practico 1

de Santiago Suarez Ortega -
Número de respuestas: 0
(1) Si x<2 en  x\sqrt{x-1\:}>\left(x-1\right)\cdot \sqrt{x-2} la inecuación no existe

 Ej.: Reemplazas x=1 en  x\sqrt{x-1\:}>\left(x-1\right)\cdot \sqrt{x-2} y te devuelve:
 
*  1\sqrt{1-1\:}>\left(1-1\right)\cdot \sqrt{1-2}
* 1\sqrt{0}>\left(0\right)\cdot \sqrt{-1} 
* 0>0 => Falso

En cambio, x=2 te devuelve: 

*  2\sqrt{2-1\:}>\left(2-1\right)\cdot \:\sqrt{2-2}
* 2>0 => Verdadero

(2) Sabiendo que la inecuación existe para  x\ge 2 : haces toda la operativa para hallar las X.

(3) Las X halladas son los "inputs" o valores de entrada que hacen Verdadera a la inecuación. Si, por el contrario, le ingresas valores distintos a éstos, la inecuación es FALSA. 
Pensálo como una PC: si le tiras valores que no puede procesar, te arroja error (FALSO) y si le das valores que puede procesar (válidos) arroja resultados (VERDADERO).