Buen día, no sé si mi respuesta a este ejercicio sea la correcta:
Capaz el tener que fundamentar que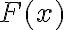 
sea creciente me ayuda con la convergencia de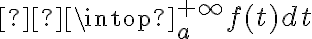 
Traté de visualizarlo mediante la proposición de que si la la integral converge, y existe el límite, entonces éste es cero (básicamente pensé que si 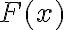está acotado, tiene un cierto límite que no puede pasar, de lo contrario no estaría acotado) aunque no sé si va por ahí la mano
Hola Alexis, la función 
no tiene por qué tener límite, no sé qué argumento usás allí para afirmar eso. Es cierto por lo visto en el teórico que si converge y tiene límite entonces este es 
, pero no tiene por qué existir este límite. No entendí cuál es la dirección que estás intentando probar, ya que usas en un momento que la integral impropia converge y luego terminás concluyendo eso. Te puede servir mirar la prueba del teorema análogo que vimos para el caso de series y usarla de inspiración para este.