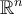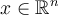Buen día.
Quería consultar sobre la respuesta (e) de la primera pregunta del cuestionario 5.
Entiendo que la lógica general de la respuesta viene por acotar el número de condición  por la norma euclídea, utilizando que
por la norma euclídea, utilizando que  , siendo
, siendo 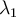 el mayor valor propio de
el mayor valor propio de 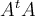 (proposición 2.5.4 en las notas, resumida en la expresión 2.9). Mi duda viene por lo descrito en la observación 2.5.4: "...incluso si
(proposición 2.5.4 en las notas, resumida en la expresión 2.9). Mi duda viene por lo descrito en la observación 2.5.4: "...incluso si  es diagonalizable, los valores propios de
es diagonalizable, los valores propios de 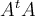 en general no son iguales a los cuadrados de los valores propios de
en general no son iguales a los cuadrados de los valores propios de  ". En este sentido quería consultar cuál era el razonamiento para asegurar que en este caso los valores propios de
". En este sentido quería consultar cuál era el razonamiento para asegurar que en este caso los valores propios de 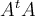 están razonablemente acotados conociendo únicamente los valores propios de
están razonablemente acotados conociendo únicamente los valores propios de  .
.
Saludos.
![[3,6] [3,6]](https://eva.fing.edu.uy/filter/tex/pix.php/040d10f86154a1502dd90b06a19ded59.png)