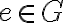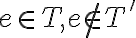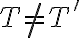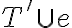Hola!
Estaba pensando un poco este ejercicio y salté con un par de ideas, y quería comentarlas para corroborarlas:
En primera instancia pensé en tomar un árbol de cubrimiento mínimo T, y suponer la existencia de otro árbol T' tal que T'!=T y luego llegar a un absurdo. En este caso haría un estilo de exchange argument, diciendo que T' = (T - e) U e', y concluir que, si puedo armar el árbol T' con otro vértice e' es porque existe un ciclo, pero, ¿sabemos que en un ciclo se elige siempre el vértice de costo mínimo? Ahí llegaríamos a que como todos los costos son distintos, y T es solución, entonces T' no es solución.
Por otra parte, se me ocurrió realizar todas las particiones posibles de todos los nodos, y luego usar el Cut Property para afirmar que, en cada partición, la arista con menor costo de S a V-S está en todo árbol de cubrimiento mínimo. Y, finalmente, de alguna forma probar que las aristas elegidas en cada partición terminan dando un conjunto único.
Agradezco cualquier comentario y corrección, gracias!!