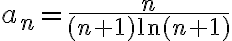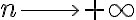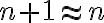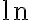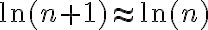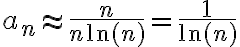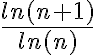Foro Práctico 4

Buenas tardes, para la parte $b)$ razoné lo siguiente: 

Por Leibnitz: 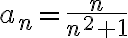$a_n = \frac{n}{n^2 + 1}$ es monótona decreciente y, además,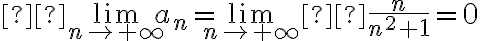 $\lim_{n\to + \infty } a_n = \lim_{n \to + \infty }  \frac{n}{n^2 + 1} = 0$

ya que 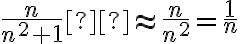$\frac{n}{n^2 + 1}  \approx \frac{n}{n^2} = \frac{1}{n}$ cuando 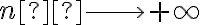$n  \longrightarrow +\infty$  , entonces cumple con las hipótesis. Luego, es convergente. Pero al evaluar la convergencia absoluta me queda: 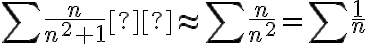$\sum \frac{n}{n^2 + 1}  \approx \sum \frac{n}{n^2} = \sum \frac{1}{n}$ , y ésta última no converge.

¿Está bien razonado de esa forma? Es decir, por el criterio sí converge (cumple ambos requisitos) pero no es una convergencia absoluta.