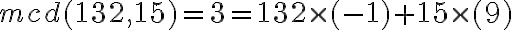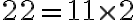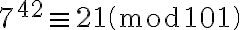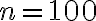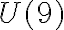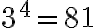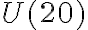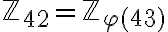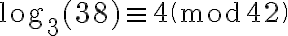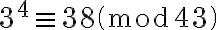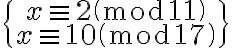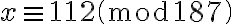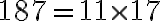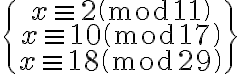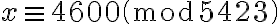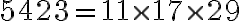Agrego a la lista anterior algunos comandos de PARI/GP que pueden ser de ayuda para los ejercicios de práctico. Recuerden que pueden utilizar esta "calculadora" accediendo a https://pari.math.u-bordeaux.fr/gp.html
- Máximo común divisor entre 132 y 15 ("greatest common divisor" en inglés): gcd(132,15)
Devuelve: 3
- Coeficientes de Bezout de 132 y 15: gcdext(132,15)
Devuelve: [-1, 9, 3].
Esto quiere decir que: 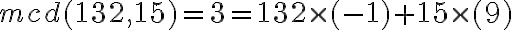 . En particular los coeficientes de Bezout que devuelve son -1 y 9. La palabra "ext" en el comando, hace alusión al algoritmo de Euclides extendido, mediante el que se calculan los coeficientes de Bezout.
. En particular los coeficientes de Bezout que devuelve son -1 y 9. La palabra "ext" en el comando, hace alusión al algoritmo de Euclides extendido, mediante el que se calculan los coeficientes de Bezout.
- Calcular la cantidad de divisores de
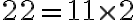 : numdiv(22)
: numdiv(22)
Devuelve: 4.
- Calcular todos los divisores positivos de 22: divisors(22)
Devuelve: [1, 2, 11, 22].
- Calcular 7^42 módulo 101: Mod(7^42,101)
Devuelve: Mod(21, 101); lo cual quiere decir que 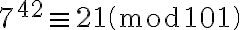
- Evaluar la función phi de Euler en
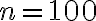 : eulerphi(100)
: eulerphi(100)
Devuelve: 40.
- Calcular el orden de la clase de equivalencia asociada al entero 4, en el grupo multiplicativo
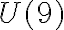 : znorder(Mod(4,9))
: znorder(Mod(4,9))
Devuelve: 3
- Calcular una raíz primitiva módulo 3^4: znprimroot(3^4)
Devuelve: Mod(2, 81); lo cual quiere decir que 2 es raíz primitiva módulo 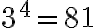 . En este comando el módulo debe ser potencia de un primo.
. En este comando el módulo debe ser potencia de un primo.
- Calcular representantes de todos los elementos del grupo multiplicativo
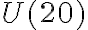 . Es decir: enteros entre 1 y 20 que son coprimos con 20.
. Es decir: enteros entre 1 y 20 que son coprimos con 20.
for (n=1, 20, if ( gcd(n,20) == 1, print1(n, " ") ) )
Devuelve: 1 3 7 9 11 13 17 19.
- Calcular el logaritmo discreto de 38 en base 3, como elemento de
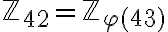 : znlog( 38, Mod(3,43) )
: znlog( 38, Mod(3,43) )
Devuelve: 4; lo cual quiere decir que: 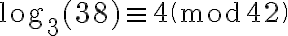 .
.
Esto equivale a decir que: 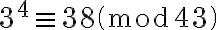 . Por lo tanto, el valor obtenido se puede verificar con el comando: Mod(3^4,43), que efectivamente devuelve Mod(38,43).
. Por lo tanto, el valor obtenido se puede verificar con el comando: Mod(3^4,43), que efectivamente devuelve Mod(38,43).
- Resolver un sistema de 2 congruencias lineales:
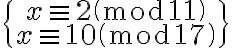 : chinese( Mod(2,11), Mod(10, 17) )
: chinese( Mod(2,11), Mod(10, 17) )
Devuelve: Mod(112, 187). Esto quiere decir que la solución del sistema es:
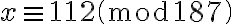
. Notar que
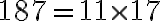
.
- Resolver un sistema de 3 congruencias lineales:
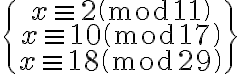 :
:
chinese( chinese( Mod(2,11), Mod(10,17) ), Mod(18,29) )
Devuelve: Mod(4600, 5423); por lo que la solución del sistema es: 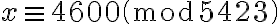 . Notar que
. Notar que 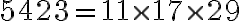 .
.
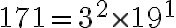 .
. es primo: isprime(n)
es primo: isprime(n)