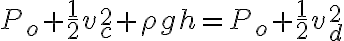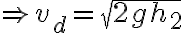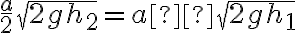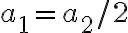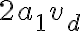Foro de Consultas Ejercicios y Teórico

Buenas noches, tengo una duda sobre este ejercicio: 

En la parte c) me pregunta sobre una nueva altura 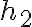$h_2$ para que los flujos volumétricos sean iguales.

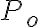La única forma de relacionar alturas que encontré es mediante Bernoulli, así que me tomé, en el tanque 2, un punto $c$ en la parte superior que está expuesta a una presión atmosférica $P_o$ , y el otro punto, 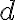$d$ es el del orificio a una altura 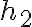$h_2$, entonces:

$P_o 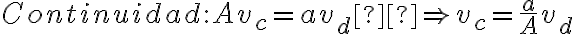+ \frac{1}{2}v_c ^{2} + \rho gh = P_o + \frac{1}{2} v_d ^2$, me queda $v_c ^2 + 2gh = v_d ^2$

Por $Continuidad : Av_c = av_d  \Rightarrow v_c = \frac{a}{A} v_d$ por lo que 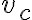$v_c$ es prácticamente despreciable (ya que $A >> a$)

$\Rightarrow v_d=\sqrt{2gh_2}$

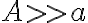Finalmente flujo volumétrico 2 es 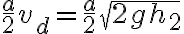$\frac{a}{2} v_d = \frac{a}{2} \sqrt{2gh_2}$

si igualo a flujo 1 me queda $\frac{a}{2} \sqrt{2gh_2} = a \sqrt{2gh_1}$

y me queda que 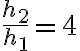$\frac{h_2}{h_1}=4$ pero la respuesta es 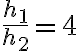$\frac{h_1}{h_2}=4$, no sé si no importa eso o algo planteé mal