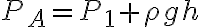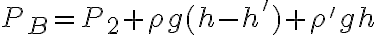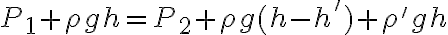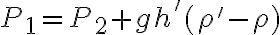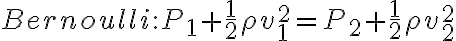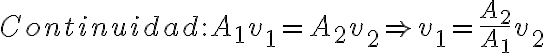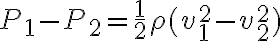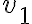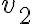F2 - 2S: Venturi y Bernoulli

Buenas tardes, en la clase 5 del teórico se dio un poco sobre el Medidor de Venturi pero no se resolvió por completo el ejercicio y no entiendo cómo seguir el hilo del desarrollo para poder despejar 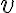$v$ .

Primero, por lo que entendí se trata de demostrar que 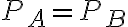$P_A = P_B$

donde $P_A = P_1 +\rho gh$

y $P_B = P_2 + \rho g(h-h') + \rho ' gh$

Entonces $P_1 + \rho gh = P_2 + \rho g(h-h') + \rho ' gh$

$P_1 = P_2 + gh' (\rho ' - \rho)$

Utilizando la fórmula de $Bernoulli: P_1 + \frac{1}{2}\rho v_1^2 = P_2 + \frac{1}{2}\rho v_2^{2}$

$Continuidad: A_1v_1=A_2v_2 \Rightarrow v_1=\frac{A_2}{A_1}v_2$

Luego ya no sé cómo proseguir

Re: Venturi y Bernoulli

de Virginia Feldman - martes, 22 de agosto de 2023, 21:02

Hola Alexis.
Fijate que de estática sacaste que

$P_1-P_2=gh'(\rho'-\rho)$ .
Por otro lado, con Bernoulli sacaste

$P_1-P_2=\frac{1}{2}\rho(v_1^2-v_2^2)$ .
Igualando estas dos expresiones hallás una relación entre velocidades, h' y densidades.
Por último, de continuidad tenés

$v_1$ en función de

$v_2$ que podés sustituir en la ecuación anterior para determinar una de las velocidades en función de los datos del problema.
Espero haber aclarado tu duda.
Saludos.