Hola Ayelén,
Primero tengo un comentario que cuando integramos en ambos lados de la igualdad es respecto a la misma variable para que se mantenga la igualdad, en este caso es respecto a . En la notación pasamos a escribir
. En la notación pasamos a escribir 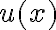 como simplemente
como simplemente  y lo mismo con su derivada, pero puede llegar a resultar útil en los primeros ejercicios que hacemos seguir escribiendo
y lo mismo con su derivada, pero puede llegar a resultar útil en los primeros ejercicios que hacemos seguir escribiendo 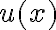 y
y 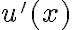 para no olvidarnos que es una función, luego que le agarramos la mano si es más sencilla la notación estándar.
para no olvidarnos que es una función, luego que le agarramos la mano si es más sencilla la notación estándar.
Luego, hay un error en el cambio de variable. Si queremos sustituir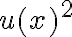 por
por 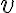 , entonces
, entonces 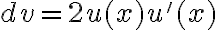 . El cambio de variable más adecuado allí es
. El cambio de variable más adecuado allí es 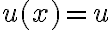 y
y 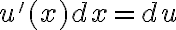 .
.
Saludos,
Leandro
Primero tengo un comentario que cuando integramos en ambos lados de la igualdad es respecto a la misma variable para que se mantenga la igualdad, en este caso es respecto a
 . En la notación pasamos a escribir
. En la notación pasamos a escribir 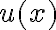 como simplemente
como simplemente  y lo mismo con su derivada, pero puede llegar a resultar útil en los primeros ejercicios que hacemos seguir escribiendo
y lo mismo con su derivada, pero puede llegar a resultar útil en los primeros ejercicios que hacemos seguir escribiendo 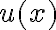 y
y 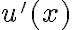 para no olvidarnos que es una función, luego que le agarramos la mano si es más sencilla la notación estándar.
para no olvidarnos que es una función, luego que le agarramos la mano si es más sencilla la notación estándar.Luego, hay un error en el cambio de variable. Si queremos sustituir
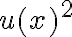 por
por 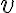 , entonces
, entonces 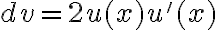 . El cambio de variable más adecuado allí es
. El cambio de variable más adecuado allí es 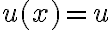 y
y 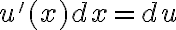 .
.Saludos,
Leandro
