hola, ahora tengo dudas con el ej 3 debido a las coordenadas, ya que en la parte b al hacer Fp=(p*nabla)Fext, el p tiene dirección k, p*nabla sería dp/dz? y que hago con el campo electrico de la carga puntual? porque sería radial, no veo cómo encajar las cosas, pero hay que hacer cambio de coordenadas por ahí
hice esto ahora, pero tengo problemas con los vectores a la hora de calcular los momentos, no sé por qué, mismo a la hora de calcular la fuerza Fp, cuando intento usar el vector r=r^r o el vector p=p^k me da cosas raras, por eso para calcular Eext tuve que ir por otro camino. Traté en ese caso de pasar el vector p usando que k=cos*r -sen*theta pero no funcionó


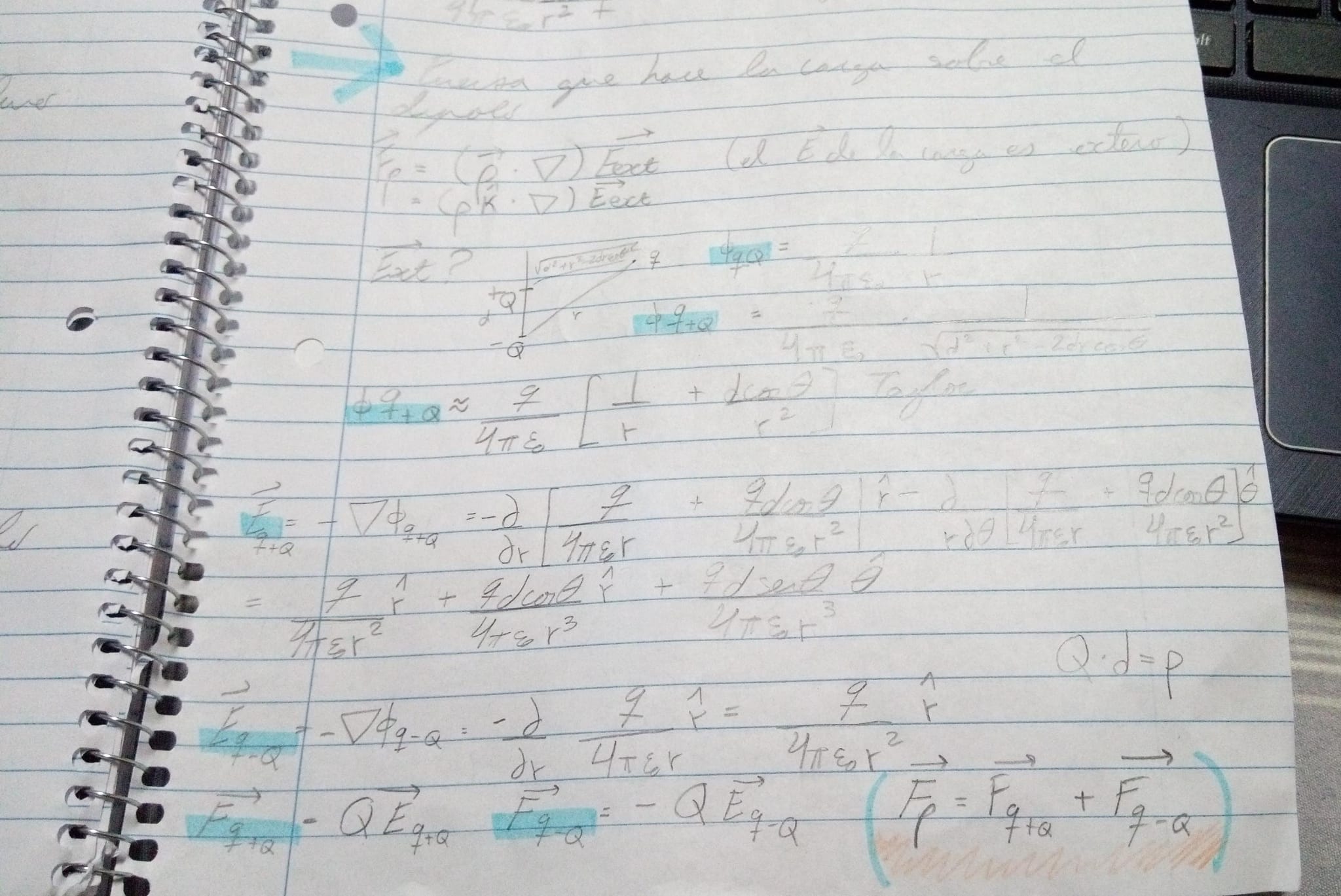

Te pide calcular la fuerza que le hace el dipolo a la carga, en este caso la fuerza es qE, donde E es el campo del dipolo.
También podes calcular la energía y hacerle el gradiente para llegar a la fuerza, creo que eso es lo que quisiste hacer, que creo que es la formula que intentas aplicar. Respecto esto, no se si te sigo pero si seria p d/dz F, ahi el d/dz debe aplicarse sobre el r que tienen 3 componentes y una de ellas es z.
En el caso de lo momentos te recomiendo usar lo deducido en clase, el momento sobre un p es p x E, siendo E el campo externo evaluado en el punto donde esta o; y el sobre una carga puntual r x F, siendo F la fuerza que sufre esa carga.
Ahora, de lo que veo abajo la F sobre q parece bien, es la carga por E. y el momento arranca bien, solo que la hacer e_r x_er da nulo, y e_r x k daría sin(theta) según e_phi, debo proyectar el e_r en un versor perpendicular a k (por eso el sin), y la componente me debe dar perp a k y la proyección, por eso el e_phi.
Fíjate si con todo eso no te destrancas....
En la parte de calcular el momento de la fuerza del dipolo sobre la carga mi problema es que me queda con el signo incorrecto, no veo por qué. En cuanto a lo otro no capto mucho lo de p d/dz porque p tiene dirección k, mi intención era descomponerlo en la dirección theta y fi, pero p.nabla me da 0 si hago eso, sin embargo no veo por qué usar coordenadas cartesianas, porque además no he usado z en ningún sitio, solo r, no sabría cómo derivar eso, mi idea era hacer p.Nabla usando esféricas pero da 0
p.namla con p según k 1ueda p d/dz, la única componente del namla que no tiene producto escalar nulo es la de z. Cuando tengo algo direccionado en z, las esféricas no son la mejor opción, r es un vector que depende de x y z, y su modulo es la raiz(x^2+y^2+z^2). Derivar respecto de z es hacer una regla de la cadena d/dz = dr/dz d/dr. Usando coordenadas móviles, hay que tener mucho cuidado en como se expresan las cosas, y es si hay que derivar versores...
Si queres usar otro sistema de coordinadas y descomponer z, usa el namla correcto para ese set
lo de p.nambla tiene sentido, pero no me causaría problemas con Eexterior? ya que mi campo Eexterior está en esféricas, lo tendría que pasar a cartesianas también?
Mas allá de si el campo de una carga puntual esta en esféricas o no, tu dipolo esta según k, y en algún momento las coordenadas esféricas no te va alcanzar. Sino, repito que intentes calcula la fuerza de interacción qq y q-q, aproximando luego cuando d/r es chico, como en la parte a.
Saludos
Si, k se puede descomponer en esfericas, segun er y e_theta. Quizas el problema esta en como tomas el namla en esfericas, como lo haces? Eso no es tan simple, en general en el curso se enfoca en ver com queda aplicado el gradiente divergencia y rotor en diferentes coordenadas y no el namla como vector. Si queres mantener ese camino y trabajar el namla com vector para ese producto escalar y luego aplicarlo al campo, lo mejor es coordenadas cartesianas.
se me había ocurrido agarrar esto:

solo que en vez de A_r pongo p*cosTheta y en vez de A_theta pongo -p*senTheta, ya que tenía descompuesto p así, pero si eso no funciona dices que haga todo el ejercicio en cartesianas? Entonces pasa saber qué coordenadas usar me fijo los vectores que me dan y no la geometría del problema? Creo que el problema está en el p porque al hacer el momento de la fuerza que la carga le hace al dipolo me da cualquier cosa. No veo mucho cómo quedaría todo en cartesianas porque el fi que hallé al principio lo hallé en función fi(r), si descompongo r en x,y,z me va quedar algo super largo el fi(x,y,z)
Este problema NO tiene simetria esferica, hay un dipolo segun k, tiene simetria de revolucion (no depende del phi, el angulo en el plano de coordenadas esfericas). Tampoco digo que hagas todo el problema en cartesianas, digo que cuando sea necesario usar la dependencia de r(z) la uses.
Creo que hay un entrevero importante (respecto a coordenadas, operados, simetrias y geometrias) que el foro no esta pudiendo solucionar, te propongo que intentes resolverlo en alguno de los practicos de forma presencial (o en el practico virtual), incluso si queres yo puedo ir 15-20 min antes a mi practico del jueves y lo vemos ahi. Solo confirmame esto asi voy antes efectivamente.
