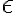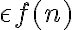Practico 2-Ejercicio 3 b)

Practico 2-Ejercicio 3 b)

de Ignacio Faget -
Número de respuestas: 1

Hola, 

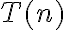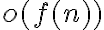no logro darme cuenta como demostrar que: Si T(n) es o(f(n)) entonces el lim \frac{T(n)}{f(n)}=0.

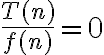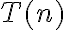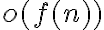Si aplico que, Si T(n) es o(f(n)), puedo decir 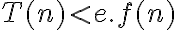T(n) < e.f(n), pero si acoto el limite por esto, me queda e, y la forma de que sea cero es que e=0. Eso no puede pasar por la def de o-chica.

Saludos, 

Ignacio.
En respuesta a Ignacio Faget

Re: Practico 2-Ejercicio 3 b)

de Alvaro Martin -
Hola.
La clave es usar que si bien ϵϵ no puede ser cero, es arbitrariamente chico, ya que la definición indica que para cualquier constante ϵ>0ϵ>0 ....
Usando la definición de límite, en particular aplicada a T(n)/f(n), llegás al resultado.

Vale la pena observar que el resultado de esta parte es una definición equivalente de o chica (que es de hecho la que hemos usado en otras oportunidades, como por ejemplo el ejercicio resuelto en clase en 2020). Efectivamente, si T(n)/f(n) tiende a cero entonces, para cualquier \epsilon positivo que nos demos, se cumple que T(n) es menor que \epsilon f(n) para n suficientemente grande.

Saludos,
Álvaro