estaba hacienod este eejr, la parte 2 no estaria llegando, no me doy cuenta de como hacerlo de una forma que no sea grafica, y de forma grafica no estaria llegando, no se si meti la pata en algun lado 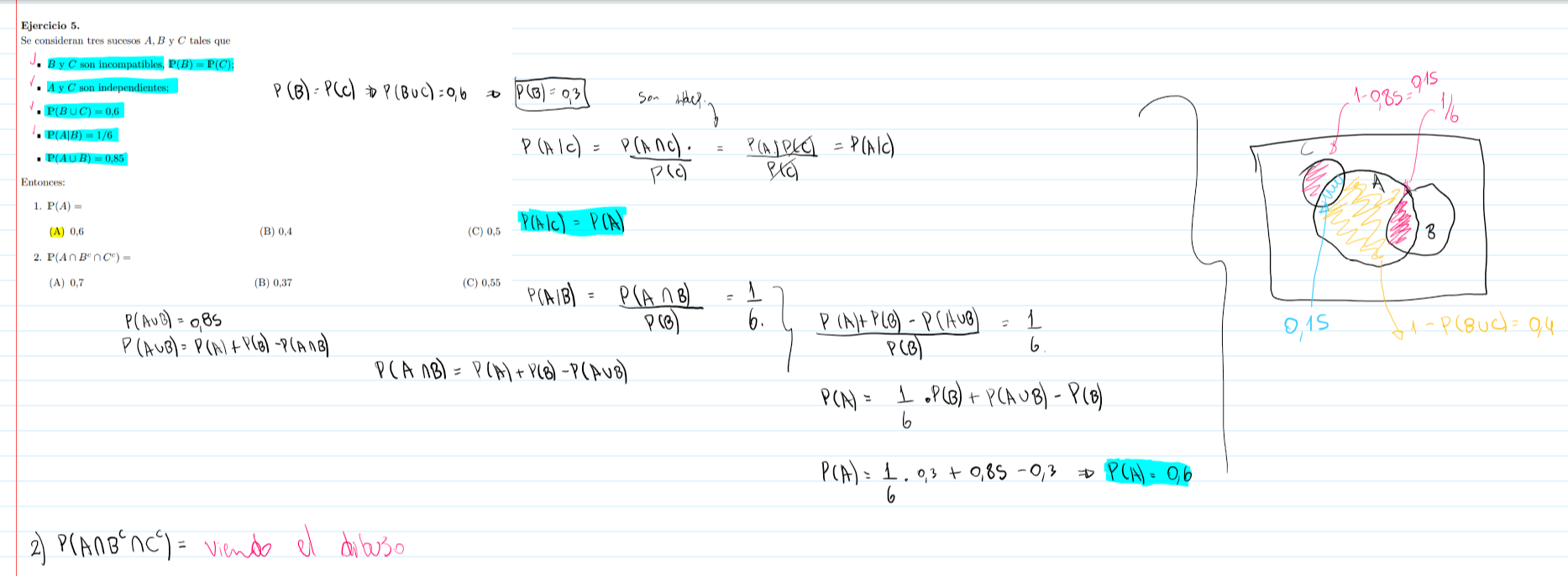
Cómo estás Nicolás?
De la parte 1, dedujiste que $$P(A) = 0,6$$, $$P(A \cap B) = 0,05$$ (un sexto de la probabilidad de B).
Ahora, como A y C son independientes, te queda que $$P(A \cap C) = P(A) . P(C) = 0,18$$, entonces $$P(A \cap B^C \cap C^C) = 0,6 - 0,05 - 0,18 = 0,37$$
Si quedó alguna duda me dices,
Saludos
De la parte 1, dedujiste que $$P(A) = 0,6$$, $$P(A \cap B) = 0,05$$ (un sexto de la probabilidad de B).
Ahora, como A y C son independientes, te queda que $$P(A \cap C) = P(A) . P(C) = 0,18$$, entonces $$P(A \cap B^C \cap C^C) = 0,6 - 0,05 - 0,18 = 0,37$$
Si quedó alguna duda me dices,
Saludos
genial, ahora si llegue, aunque me genera un poco de duda que que no se pueda hacer por el dibujo que plante arriba, yo no me habia dado cuenta de poner la codincion de independencia entre a y c (P(A∩C)=P(A).P(C)=0,18).
pero P(AuB)=0,85, eso no me esta diciendo que la probabilidad que esta en C (sacando lo que esta en A) no es de la forma 1-0,85=0,15?
dejo un dibujito
pero P(AuB)=0,85, eso no me esta diciendo que la probabilidad que esta en C (sacando lo que esta en A) no es de la forma 1-0,85=0,15?
dejo un dibujito
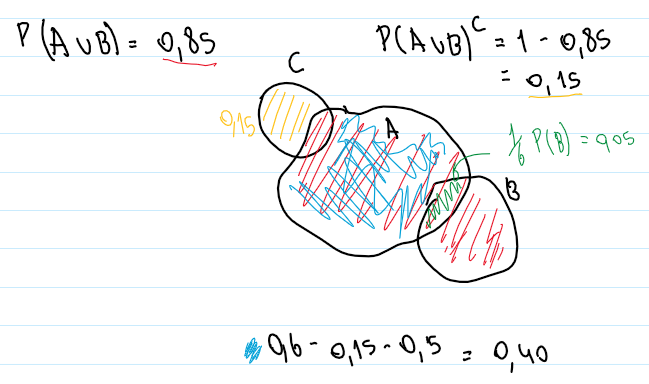
Buenas Nicolás,
Sí lo podés hacer con dibujito, nomás fijate que $$(A \cup B)^C$$ también incluye elementos que no están en $$C$$, por eso no podés despejar lo que querés.
Saludos
Sí lo podés hacer con dibujito, nomás fijate que $$(A \cup B)^C$$ también incluye elementos que no están en $$C$$, por eso no podés despejar lo que querés.
Saludos
genial gracias
