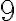Buenas noches en la solución del parcial v2 en el ejércicio uno hay un error pues se dice que el tamaño máximo de la anticadena es de 4 sin embargo no aparece el número 9 con el cual la anticadena quedaría de 5 y la respuesta sería la e
Me sumo a lo que plantea el compañero. Yo encontré (por definición de anticadena) A={6,7,8,9,10} una anticadena cuyo largo es 5!
En respuesta a Valentín Pedragosa Groba
Re: Solución segundo parcial
En la v1 puede observar el mismo error, {4 6 9 10 7 } es una anticadena y tiene tamaño 5.
En respuesta a Valentín Pedragosa Groba
Re: Solución segundo parcial
Me sumo a la queja, yo plantee una anticadena 4-6-9-10-7 de tamaño 5. NInguno de esos números está relacionado entre si, ya que ninguno es múltiplo del otro.
En respuesta a Valentín Pedragosa Groba
Re: Solución segundo parcial
Me sumo al foro, tuve el mismo problema, la cadena mas larga que encontré seria { 4 6 9 10 7 } en la versión 2
En respuesta a Valentín Pedragosa Groba
Re: Solución segundo parcial
concuerdo con la queja, La respuesta es la e.
Me sumo al planteo del compañero
Me sumo a lo que plantean los compañeros. Version 2 la respuesta es E.
También pienso que la respuesta es la e. Por decir otro ejemplo 4 5 6 7 9 es una anticadena de 5 elementos. Además en la resolución del problema plantea una descomposición en cadenas que omite el elemento 9.
Buenas!!
adhiero a la consulta
en la v1 yo encontre el subconjunto {8,6,9,10,7) en el que ninguno esta relacionado con ninguno, creo que entraria en la definicion de anticadena y seria de 5
saludos!
adhiero a la consulta
en la v1 yo encontre el subconjunto {8,6,9,10,7) en el que ninguno esta relacionado con ninguno, creo que entraria en la definicion de anticadena y seria de 5
saludos!
En respuesta a Valentín Pedragosa Groba
Re: Solución segundo parcial
Me sumo a lo que planteo el compañero.
En respuesta a Valentín Pedragosa Groba
Re: Solución segundo parcial
Yo la verdad considero que a este punto este ejercicio parece ser la fuente de ub descontento y de falsas esoeranzas en mas de una persona
Concuerdo. Y en la solucion donde pone
"Por ultimo, notemos que el conjunto {2, 3, 5, 7} es una anticadena de tamaño 4, y que existe alguna partición de A en 4 cadenas, por ejemplo {1, 2, 4, 8, 0}, {3, 6}, {5, 10}, {7}. Por el Teorema de Dilworth se sigue que la anticadena de tamaño maximo 4"
Ahi creo que el 0 deberia estar aparte, porque no es comparable con nadie no? Porque el n de la condicion de la relacion "b = n*a" era mayor o igual que 1. Y si el 0 esta aparte ahi si serian 5 cadenas, y puede haber una anticadena tamaño 5 segun el teorema ese
"Por ultimo, notemos que el conjunto {2, 3, 5, 7} es una anticadena de tamaño 4, y que existe alguna partición de A en 4 cadenas, por ejemplo {1, 2, 4, 8, 0}, {3, 6}, {5, 10}, {7}. Por el Teorema de Dilworth se sigue que la anticadena de tamaño maximo 4"
Ahi creo que el 0 deberia estar aparte, porque no es comparable con nadie no? Porque el n de la condicion de la relacion "b = n*a" era mayor o igual que 1. Y si el 0 esta aparte ahi si serian 5 cadenas, y puede haber una anticadena tamaño 5 segun el teorema ese
Hola, Marcelo.
En el ejercicio el valor de
podía ser 
, con lo cual el está relacionado con todos los otros elementos.
El error en la solución es que faltó incluir al
, que en la partición en cadenas se podría agregar como una quinta cadena que lo contenga a él solo.
En el ejercicio el valor de
podía ser , con lo cual el está relacionado con todos los otros elementos.El error en la solución es que faltó incluir al
, que en la partición en cadenas se podría agregar como una quinta cadena que lo contenga a él solo.Hola, estudiantes.
Es como ustedes dicen, hay un error en la solución y el tamaño máximo de una anticadena es 5. ¡Gracias por notarlo!
En breve haremos la corrección en las soluciones que subimos.
Es como ustedes dicen, hay un error en la solución y el tamaño máximo de una anticadena es 5. ¡Gracias por notarlo!
En breve haremos la corrección en las soluciones que subimos.
Buenas noches, luego de conversar los resultados con algunos compañeros llegamos a que quizás pueda existir una confusión con respecto a la definición de tamaño de una cadena. Según lo dado en el teórico, el tamaño de una cadena (o anticadena en este caso) es el numero de aristas que la componen, mientras que por otro lado llamamos orden de una cadena al número de elementos o vértices que la componen. Por lo que el conjunto {10,9,8,7,6} es una antidacena de tamaño=4 y orden=5 siendo la respuesta correcta la D en lugar de la E (en la versión 1 del parcial) como se planteo en un principio.
Estoy de acuerdo con el compañero Iván, el término orden es quien hace referencia a la cantidad de elementos de la anticadena. En este caso, los elementos que determinan el tamaño de una anticadena son: {(10,9);(9,8);(8,7);(7,6)}
Estoy de acuerdo con el razonamiento de Iván y Matias
Claro, pero tambien tenes que tener en cuenta lo que dice el teorema de dilworth, la forma de cubrir el diagrama utilizando cadenas es igual al ancho del diagrama que a su vez es igual a el cardinal de la anticadena mas larga y en este caso tenes que utilizar una cantidad de 5 cadenas para cubrir el diagrama. Tengo entendido que se cumplen estas igualdades. Ademas ten en cuenta que no se presenta una ¨arista¨ en una anticadena, porque los elementos no estan relacionados.
En respuesta a Iván Santavec Bovio
Re: Solución segundo parcial
según https://eva.fing.edu.uy/course/view.php?id=1541§ion=10 tamaño o cardinal refieren a la cantidad de elementos de una cadena. Asumo que lo mismo aplica a una anticadena
Estoy totalmente de acuerdo contigo. En mi practico habiamor realizado tal ejercicio no tan distinto al presentado en el parcial y de la misma forma que se resolvió en el practico, fue lo q realice en el parcial y aplique lo que en mi practico habiamos definido como el tamaño máximo de una anticadena y no veia manera de que fuese 5. Yo creo q aca difiere mas en como fue explicado en las clases lo que es una anticadena y creo que aqui es donde nace el problema de porque algunas personas tienen una respuesta y otros otra.
Hola Iván. Una anticadena por definición no tiene aristas (salvo obviamente los lazos implícitos) por lo que no hay forma de confundirse por ese lado. Además en el teorema de Dilworth y los ejemplos que se vieron del mismo en clase queda claro que el tamaño es la cantidad de elementos.
Saludos,
Gabriel
Saludos,
Gabriel
Tal cual. Una anticadena es un conjunto en el que ninguno de los elementos se relacionan por ende no existe aristas entre ellos, el largo corresponde a la cantidad de elementos que tiene el conjunto y fue así como se dio en el curso.
En respuesta a Valentín Pedragosa Groba
Re: Solución segundo parcial
Estoy de acuerdo con Ivan y con Matías, además definimos en teórico como “tamaño” de un camino a la cantidad de aristas que lo componen, por lo que la afirmación: “tamaño de la anticadena”. se presta a confusión.
Buenas a todas/os,
Agradezco por haber iniciado este hilo de comentarios y quejas. Tienen razón quienes indicaron que existe una anticadena de tamaño 5, y que en consecuencia la respuesta correcta es la E. Pueden encontrar un fundamento a esta respuesta en este link.
Agradezco por haber iniciado este hilo de comentarios y quejas. Tienen razón quienes indicaron que existe una anticadena de tamaño 5, y que en consecuencia la respuesta correcta es la E. Pueden encontrar un fundamento a esta respuesta en este link.
Fue actualizada la solución de ambas versiones.
Como docente responsable del curso van mis disculpas por los inconvenientes que hemos generado.
Cordiales saludos,
Pablo.