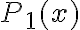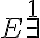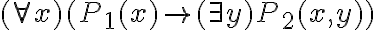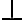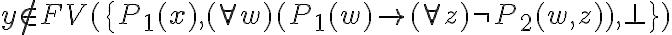Hola, por qué en el (*4) chequea la hipótesis de arriba a la izquierda del todo? Entiendo que en la eliminación del existe solo se deben chequear que y no esté en las FV de bottom ni en las hipótesis sin cancelar de la rama derecha de la eliminación.
Buenas:
Hay que tener cuidado cuando considerás las hipótesis canceladas, que esas hipótesis estén efectivamente canceladas en el subárbol que se está considerando.
En este ejemplo, cuando se aplica la eliminación del existe (*4), la hipótesis 
no se considera cancelada.
Esto se debe a que esa hipótesis se cancela con la regla 
que está más abajo y por lo tanto no está cancelada
en el subárbol que estamos considerando.
Nicolás, ahora entiendo lo que preguntás.
Tenés razón, la fórmula:
no aparece en el árbol correspondiente a la derivación de 
para la introducción de existe (*4). No debería ser considerada.
La justificación debería ser:
