Buenas
Las afirmaciones son relativas a la continuidad de la función  . Voy a "traducirlas" en términos de continuidad pero no probar aun. Si no sabes como verificar si son ciertas o no vuelve a escribir
. Voy a "traducirlas" en términos de continuidad pero no probar aun. Si no sabes como verificar si son ciertas o no vuelve a escribir
Como 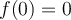 . La afirmación I es la definición de la continuidad de
. La afirmación I es la definición de la continuidad de  es
es 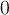
Como 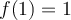 . La afirmación II es la definición de la continuidad de
. La afirmación II es la definición de la continuidad de  es
es 
La condición III es equivalente a que  este acotada en un entorno de
este acotada en un entorno de  . Veamos que esta ultima es verdadera.
. Veamos que esta ultima es verdadera.
Observa que empieza con un existe 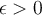 podemos tomar entonces un valor muy grande, por ejemplo 10. Para ese valor me preguntan si existe un
podemos tomar entonces un valor muy grande, por ejemplo 10. Para ese valor me preguntan si existe un 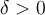 tal que
tal que  para todo
para todo  . Al haber tomado un valor tan grande en
. Al haber tomado un valor tan grande en 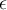 , sera fácil encontrar en este caso un valor de
, sera fácil encontrar en este caso un valor de 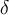 que cumpla la propiedad. Puedes verificar que
que cumpla la propiedad. Puedes verificar que  lo cumple.
lo cumple.
Si tienes dudas de como verificar esto ultimo con la propiedad III o como probar la continuidad o no continuidad en las anteriores vuelve a escribir
Saludos