¡Buenas!
Te intentaré responder con lo que entiendo:
En la parte A lo que sucede es que estás pasando del mundo sintáctico al mundo semántico. No es lo mismo decir que dos elementos de un conjunto son "iguales prima", a decir que las interpretaciones de dichos elementos en una estructura son iguales (es un poco confuso pues los símbolos son similares, pero ā es distinto de a, y b̄ es distinto de b. "ā" es, en este caso, un elemento de FORM, mientras que "a" es la interpretación de ese mismo elemento en la estructura "M").
En la parte B; sí; justamente es porque P es un conjunto. De hecho, P *siempre* es un conjunto, no solamente en este caso. P siempre es el conjunto de los elementos del universo que cumplen una determinada propiedad (la propiedad que los hace pertenecer a P). Ejemplos;
Si tenés la estructura M1=<N, Par>, donde el universo N es el conjunto de los naturales, y Par es la propiedad de "ser un número par", entonces P es el conjunto de los números que cumplen la propiedad de ser pares (el conjunto Par = {0,2,4,6,8, ...}).
Si tenés la estructura M2=<ABC,Voc> donde el universo ABC = {a,b,c,d,e, ... x,y,z} y Voc es la propiedad de "ser una vocal", entonces Voc es el conjunto Voc={a,e,i,o,u}.
Otra forma de pensarlo es pensarlo así:
M2 = <{a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z},{a,e,i,o,u}>. Como es demasiado largo, simplemente ponemos <ABC, Voc>.
del mismo modo: M1 = <{0,1,2,3,4,5, ...}, {0,2,4,6,8,...}>. Como son infinitos, ponemos <N, Par>.
Toda relación P es un subconjunto del universo U. En los ejemplos que di, P es una relación unaria (ser par, ser vocal). En los casos en que P es una relación binaria, P no es un subconjunto de U, sino un subconjunto de UxU. Si fuese una relación que recibe tres parámetros, sería un subconjunto de UxUxU ... etc.
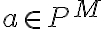 , ¿es porque se trata de un conjunto? Si no fuese un conjunto ¿que se pondria?
, ¿es porque se trata de un conjunto? Si no fuese un conjunto ¿que se pondria?


