Foro de parciales y exámenes anteriores

Hola Santiago, recuerda que si 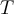$T$ es ortogonal entonces las raíces del polinomio característico deben tener modulo = 1.

En este caso las raíces son $\lambda=4,\;\lambda=1$, por tanto no puede ser ortogonal (sí es diagonalizable).

Para ver que 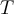$T$ es autoadjunto, encuentra una base de vectores propios y luego encuentra un producto interno para el cual dicha base de vectores propios sea ortonormal (puedes verlo en el ejercicio 11 del práctico 5).

Entonces tendrás una base ortonormal en la que la matriz asociada queda diagonal (y por tanto simétrica), y por tanto 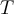$T$ es autoadjunto.

Saludos

J.