Hola:
En la derivación de la derecha, la clave está en encontrar la sustitución
apropiada para la eliminación del para todo
con la hipótesis ![\forall y (x =' y \to \varphi[y/x]) \forall y (x =' y \to \varphi[y/x])](https://eva.fing.edu.uy/filter/tex/pix.php/e2629d70e17f4017bee57be78b7ab831.gif) .
.
Aquí te recomiendo que busques un término  para sustituir
la
para sustituir
la  de manera que te quede algo así:
de manera que te quede algo así:
donde:
Con eso sale fácil.

![x ='t \to \varphi[t/x] x ='t \to \varphi[t/x]](https://eva.fing.edu.uy/filter/tex/pix.php/7df233f2b96f66b5e3c5b167d98e4578.gif)
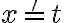
![\varphi[t/x] \varphi[t/x]](https://eva.fing.edu.uy/filter/tex/pix.php/cd7a45bc877336b3f14d360a177ee6ba.gif)
