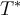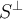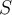5.1

5.1

de Nataly Melanie Ruber Maimo -
Número de respuestas: 6

hola. Ortonormalicé las bases x^2 +x + 1 y la base  x + 1 para usarlas en este ejercicio, pero no termino de poder usarlas correctamente para solucionarlo. Mi primer idea fue hacer

<T(x^2 + x + 1), 1> = <(x^2 + x + 1), T*(1)>

y usar <T(x^2 + x + 1), 1> = <(x^2 + x + 1), T*(x-(1/2)√12)>

pero no da, con {1, x-(1/2)√12} base de R1[x] por las dudas.

Creo que el problema está en usar T(x^2 + x + 1), ya tengo la base de R2[x] ortonormalizada así que eso no es problema pero no sé si usarla aquí, me queda algo muy largo y es confuso, querría si me pudieran orientar porfavor

En respuesta a Nataly Melanie Ruber Maimo

Re: 5.1

de Lucas Nahuel De Leon Machado -
Buenas,

como ya tienes la base ortonormal de R2[x], te recomiendo mirar el ejercicio 3 y ver si alguna de las propiedades te puede servir.

Saludos.
En respuesta a Lucas Nahuel De Leon Machado

Re: 5.1

de Nataly Melanie Ruber Maimo -
Okey creo que ya entendí. Con la propiedad 1 queda mucho más sencillo y ahora pude llegar a algo aparentemente correcto, lo probé con algunos ejemplos y funciona. Así que usaría ese método cuando me encuentre con algo complicado
Por otro lado, aprovecho para preguntar si hice bien la parte 2. La probé con un ejemplo sencillo y me funcionó pero tengo mis dudas de si está bien
lo que hice fue hacer
<T(A),B>=<A,T*(B)>
<At+A,B>=<A,T*(B)>
tr((At+A)*Bt) = tr(A*(T*(B)t))
tr(At *Bt)+ tr(A*Bt) = tr(A*T*(B)t))=tr(A*(a+b)t)=tr(A*at)+tr(A*bt)
a=(A-1)t*A*B
b=B
T*=a+b= (A-1)t*A*B + B
En respuesta a Nataly Melanie Ruber Maimo

Re: 5.1

de Lucas Nahuel De Leon Machado -
Ojo que la cuenta que hiciste asume que A es invertible, y otra cosa que te puede decir que dio algo raro es que fíjate que T^* te quedó dependiendo de quien sea A.
Este también se puede encarar como el anterior usando el ejercicio 3.1.

Sino en la misma linea de que lo que planteaste: para todas A,B\in\mathbb{R}^{n\times n} (La idea va a ser ver como queda T^*(B)):

\langle A^t + A, B\rangle=\langle A,T^*(B)\rangle,

y a la vez (¿Qué propiedades uso en la siguiente cuenta?):

\langle A^t + A, B\rangle=tr(AB)+tr(A^tB)=tr(AB)+tr(B^tA)=tr(BA)+tr(B^tA)=\langle B+B^t, A\rangle

Entonces, ¿Quién es T^*?

Otra idea (Usando proyección ortogonal):
Primero del practico anterior acordate que si S\subset\mathbb{R}^{n\times n} es el espacio de las matrices simétricas, entonces S^\perp es el espacio de las matrices antisimétricas. Y que toda A\in\mathbb{R}^{n\times n} se puede escribir como

A=\frac{1}{2}(A+A^t)+\frac{1}{2}(A-A^t),

donde \frac{1}{2}(A+A^t)\in S y \frac{1}{2}(A-A^t)\in S^{\perp}. Por tanto la proyección ortogonal de A en S es P_S(A)=\frac{1}{2}(A+A^t). Luego ¡T=2\,P_S!.
Entonces usando alguna parte del ejercicio 3, T^*(B)\in S  para toda B\in\mathbb{R}^{n\times n} (¿Por qué?) (o lo que es lo mismo Im(T^*)\subset S).

Ahora para todas A,B\in\mathbb{R}^{n\times n} (la idea va a ser ver como queda T^*(B)):

\langle A^t + A, B\rangle=\langle A,T^*(B)\rangle,

en particular para A simétrica,

0=\langle2A,B-\frac{1}{2}T^*(B)\rangle (¿Por qué?)

por lo tanto se cumple B-\frac{1}{2}T^*(B)\in S^{\perp} (¿Por qué?) y \frac{1}{2}T^*(B)\in S para toda B\in\mathbb{R}^{n\times n}. 
Recordando el practico anterior esto ultimo te debería dar para determinar quien es T^*.
En respuesta a Lucas Nahuel De Leon Machado

Re: 5.1

de Nataly Melanie Ruber Maimo -
Hola, pero el PI te debería dejar al B con traspuesta o no? porque era lo que me complicaba, digo en esta parte
⟨At+A,B⟩=tr(AB)+tr(AtB) no debería ser ⟨At+A,B⟩=tr(ABt)+tr(AtBt) ? 

(Editado por Lucas Nahuel De Leon Machado - envío original martes, 30 de mayo de 2023, 19:15)

En respuesta a Nataly Melanie Ruber Maimo

Re: 5.1

de Lucas Nahuel De Leon Machado -
Si, ahí le erré. Igual la cuenta es análoga:

\langle A + A^t, B\rangle = tr(AB^t)+tr(A^tB^t)=tr(AB^t)+tr(BA)

y a partir de ahí se sigue igual.